



Jacek Gondzio (University of Edinburgh)
I shall address recent challenges in optimization, including problems which originate from the “Big Data” buzz. The existing and well-understood methods (such as interior point algorithms) which are able to take advantage of parallelism in the matrix operations will be briefly discussed. The new class of methods which work in the matrix-free regime will then be introduced. These new approaches employ iterative techniques such as Krylov subspace methods to solve the linear equation systems when search directions are computed. Finally, I shall comment on the well-known drawbacks of the fashionable but unreliable first-order methods for optimization and I shall suggest the parallelisation-friendly remedies which rely on the use of (inexact) second-order information.
Matthew Knepley (University of Chicago)
A common pitfall in large, complex simulations is a failure of convergence in the nonlinear solver, typically Newton's method or partial linearization with Picard's method. We present a framework for nonlinear preconditioning, based upon the composition of nonlinear solvers. We can define both left and right variants of the preconditioning operation, in analogy to the linear case. Although we currently lack a convincing convergence theory, we will present a powerful and composable interface for these algorithms, as well as examples which demonstrate their effectiveness.
Dave A. May (ETH Zurich), Jed Brown (Argonne National Laboratory), Laetitia Le Pourhiet (UPMC)
Complex multi-scale interactions characterize the dynamics of the Earth. Resolving three-dimensional structures and multi-physics processes over a wide range of spatio-temporal scales is a unifying grand challenge common to all branches of Earth science and one which must be addressed in order to achieve a comprehensive understanding of the Earth and other planets.
Numerical modeling has become an important technique to develop our understanding of the Earth as a coupled dynamical system - linking processes in the core, mantle, lithosphere, topography and the atmosphere. Computational geodynamics focuses on modeling the evolution of rocks over million year time spans. Such long-term evolution of rocks is governed via the equations describing the dynamics of very viscous, creeping flow (i.e. Stokes equations). The constitutive behavior of rocks over these time scales can be described as a visco-elasto-plastic material. Due to the strong temperature dependence and the presence of brittle fractures, the resulting effective non-linear viscosity can possess enormous variations in magnitude (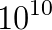 Pa s), which may occur over a wide range of length scales ranging from meters to kilometers.
Pa s), which may occur over a wide range of length scales ranging from meters to kilometers.
Of critical importance in performing 3D geodynamic simulations with sufficient rheological complexity is the preconditioner applied to the variable viscosity Stokes operator. The efficiency and robustness of this preconditioner ultimately controls the scientific throughput achievable and represents the largest computational bottleneck in all geodynamic software.
In this presentation, I outline a flexible Stokes preconditioning strategy which has been developed within pTatin3d – a finite element library specifically developed to study the long term evolution of the mantle-lithosphere.
We have made a number of fundamental design choices which result in a fast, highly scalable and robust Q2P1 finite element implementation which is suitable for solving a wide range of geodynamic applications. Specifically these choices include: (i) utilizing an inf-sup stable mixed finite element (with a unmapped pressure space) which provides a reliable velocity and pressure solution; (ii) expressing the problem in defect correction form so that Newton-like methods can be exploited; (iii) making extensive use of matrix- free operators that exploit local tensor products to drastically reduce the memory requirements, improve performance by 5-10x to attain 30% of Haswell FPU peak using AVX/FMA intrinsics, and improve on-node scalability of the sparse matrix-vector product; (iv) deferring a wide range of choices associated with the solver configuration to run-time.
The performance of the hybrid preconditioning strategy will be presented by examining the robustness of the preconditioner with respect to the topological structure and spatial variations within the viscosity field, together with its parallel scalability. In particular we will highlight the benefits of using hybrid coarse grid hierarchies, consisting of a mixture of Galerkin, assembled and matrix-free operators. Lastly, examples of 3D continental rifting will be presented to demonstrate the efficiency of the new methodology.
Mark Adams (Lawrence Berkeley National Laboratory), Matt Knepley (University of Chicago), Jed Brown (Argonne National Laboratory)
We discuss the use of segmental refinement (SR) to optimize the performance of multigrid on modern architectures by requiring minimal communication, loop fusion, and asynchronous processing, with minimal additional work with textbook efficient multigrid algorithms. We begin by continuing the work of Brandt and Diskin (1994) by investigating the robustness and quantitative work costs of SR and consider extensions of the techniques to multi-scale analysis methods.
Oliver Rheinbach (Freiberg University of Mining and Technology), Axel Klawonn (University of Cologne), Martin Lanser (University of Cologne)
The solution of nonlinear problems requires fast and scalable parallel solvers. FETI-DP (Finite Element Tearing and Interconnecting) domain decomposition methods are well known parallel solution methods for problems from partial differential equations. Recently, different nonlinear versions of the well-known FETI-DP methods for linear problems have been introduced. In these methods the nonlinear problem is decomposed before linearization. This can be viewed as a strategy to localize computational work and extend scalability in the spirit of, e.g., the ASPIN approach. We show preliminary parallel scalability results for up to 262144 processor cores on the Mira BlueGene/Q supercomputer at Argonne National Laboratory.
Johannes Steiner (Università della Svizzera italiana), Rolf Krause (Università della Svizzera italiana )
For the simulation of structural mechanics the finite element method is one of the most used, if not the most popular discretization method. In fluid dynamics the finite volume method is a widely used multi-purpose method. Therefore the coupling of finite element and finite volume methods for Fluid-Structure-Interaction is of substantial interest. We present the coupling of these two different discretization methods for Fluid-Structure-Interaction using a monolithic approach. Typically for the coupling of two different discretization methods a partitioned coupling scheme is used, where the two sub-problems are handled separately with some exchange of data at the interface. In a monolithic formulation however, the transfer of forces and displacements is fulfilled in a common set of equations for fluid and structure, which is solved simultaneously. For complex simulation domains, we end up in algebraic systems with a large number of degrees of freedom, which makes the use of parallel solvers mandatory. Here, a good choice for an efficient preconditioning strategy is important. Our solver strategies are based on the application of Newton’s method using iterative solvers within different multi-level methods. The multi-level methods are constructed on a nested hierarchy of unstructured nested meshes. We discuss both, the coupling approach of the two different discretizations as well as the efficient solution of the arising large nonlinear system.
Simone Deparis (EPFL), Gwenol Grandperrin (EPFL), Radu Popescu (EPFL), Alfio Quarteroni (EPFL)
We present two strategies for preconditioning unsteady Navier-Stokes equations discretised by the finite element method suited for parallel computing. The first one relies on an inexact block factorisation of the algebraic system, like SIMPLE, Pressure-Correction Diffusion (PCD), or Yosida, and on the approximation of the blocks by a 2-level Schwarz preconditioner or a multigrid one. We compare the different choices — SIMPLE, PCD, and Yosida — with respect to robustness and scalability. The parallelism is achieved by partitioning the finite element mesh into the same number as the available processes. With the same ideas, we develop preconditioners for fluid-structure interaction in hemodynamics and present the scalability of the new defined algorithms. The second strategy is based on Schwarz type preconditioners and on assigning a fixed small amount of processes per partition. On each subdomain, the exact or inexact resolution of the local problem is solved in parallel by either a parallel direct method or an iterative one. We present the results on cases relevant to vascular flow simulations using Trilinos and the LifeV finite element libraries.
Matthias Mayr (Technische Universität München), Michael W. Gee (Technische Universität München)
The numerical analysis of fluid-structure interaction problems has been a field of intensive research for years and plays an important role in engineering applications of all kind. Especially, the coupling of incompressible fluid flow and deformable structures undergoing large deformations is of particular interest. When it comes to real world applications, it is crucial to make predictions about the physical problem at hand very accurately, but still efficiently and with reasonable costs. With respect to temporal discretization, one has to take care of certain aspects in order to obtain an accurate, consistent and efficient scheme.
When using different time integration schemes in the fluid and structure field as done in most applications, it is not guaranteed that the equilibrium in both fields is evaluated at exactly the same time instance. Hence, the coupling tractions that are exchanged at the interface do not match in time leading to a temporal inconsistency among the fields. We have incorporated temporal interpolations of the interface tractions in our monolithic solver and, thus, allow for an independent and field-specific choice of time integration schemes in fluid and structure field in a consistent manner [Mayr et al., SIAM J. Sci. Comput., 2014 (submitted)].
When looking at accuracy and using constant time step sizes 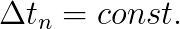 in all time steps, a high level of temporal accuracy can only be achieved by choosing overall small time step sizes. However, this leads to a tremendous increase in computational time, especially when such small time step sizes are not necessary throughout the entire simulation in order to maintain the desired level of accuracy. By choosing the time step sizes
in all time steps, a high level of temporal accuracy can only be achieved by choosing overall small time step sizes. However, this leads to a tremendous increase in computational time, especially when such small time step sizes are not necessary throughout the entire simulation in order to maintain the desired level of accuracy. By choosing the time step sizes 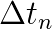 adaptively and individually for each time step
adaptively and individually for each time step 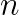 , the local discretization error of the applied time integration scheme can be limited to a user-given bound and, thus, one can achieve the desired level of accuracy by simultaneously limiting the computational costs. Therefore, we combine established error estimation procedures in the structure and fluid field (see e.g. [Zienkiewicz et al., Earthquake Engng. Struct. Dyn. (20), pp. 871-887, 1991], [Gresho et al., SIAM J. Sci. Comput. (30), pp. 2018-s2054, 2008], [Kay et al., SIAM J. Sci. Comput. (32), pp. 111-128, 2010]) to build an adaptive time stepping algorithm for fluid-structure interaction problems. This algorithm is integrated into the monolithic solver framework proposed in [Mayr et al., 2014]. By controlling the local temporal discretization error in the structure and fluid field, an optimal time step size can be selected that satisfies the accuracy demands in both fields.
, the local discretization error of the applied time integration scheme can be limited to a user-given bound and, thus, one can achieve the desired level of accuracy by simultaneously limiting the computational costs. Therefore, we combine established error estimation procedures in the structure and fluid field (see e.g. [Zienkiewicz et al., Earthquake Engng. Struct. Dyn. (20), pp. 871-887, 1991], [Gresho et al., SIAM J. Sci. Comput. (30), pp. 2018-s2054, 2008], [Kay et al., SIAM J. Sci. Comput. (32), pp. 111-128, 2010]) to build an adaptive time stepping algorithm for fluid-structure interaction problems. This algorithm is integrated into the monolithic solver framework proposed in [Mayr et al., 2014]. By controlling the local temporal discretization error in the structure and fluid field, an optimal time step size can be selected that satisfies the accuracy demands in both fields.
In the presentation, the proposed time stepping scheme for the monolithic fluid-structure interaction solver will be given and examples will be provided, that demonstrate the behaviour of the newly proposed method with respect to accuracy and computational costs.
Thomas Richter (Heidelberg University), Stefan Frei (Heidelberg University)
We present a model for fluid-structure interactions that is completely based on Eulerian coordinate systems for fluid and structure. This model is strictly monolithic and allows for fully coupled and implicit discretization and solution techniques. Without the need for artificial transformation of domains, the Fully Eulerian model can deal with very large deformations and also contact. For capturing the interface between solid- and fluid-domain we present the Initial Point Set, an auxiliary function that allows to relate the structural stresses to the reference configuration. Similar to front-capturing techniques for multiphase-flows, the great computational challenge is the accurate discretization close to the interface. Here, we introduce a novel locally modified finite element method, that resolves the interface by a special parametric setup of the basis functions. We can show optimal order convergence and also a robust condition number independent of the interface location. Further, and in contrast to established interface-resolving methods like XFEM, the number of unknowns and the algebraic structure of the system matrix also does not depend on the interface location. This helps to design efficient solvers for problems with moving interfaces.
Michael A. Heroux (Sandia National Laboratories)
Extreme-scale computers present numerous challenges to linear solvers. Two major challenges are resilience in the presence of process loss and effective scaling of robustly preconditioned iterative methods on high bandwidth, high latency systems. In this presentation, we give an overview of several resilient computing models and their use with preconditioned iterative methods. These models enable effective iterative solutions in the presence of large variability in collectives performance, process loss and silent data corruption. We also present a new framework for effectively using traditional additive Schwarz preconditioners with communication-avoiding iterative methods, addressing one of the critical shortcomings to widespread use of these approaches.
Erin Carson (University of California, Berkeley), Sam Williams (Lawrence Berkeley National Lab), Michael Lijewski (Lawrence Berkeley National Lab), Nicholas Knight (University of California, Berkeley), Ann S. Almgren (Lawrence Berkeley National Lab), James Demmel (University of California, Berkeley)
Many large-scale numerical simulations in a wide variety of scientific disciplines use the geometric multigrid method to solve elliptic and/or parabolic partial differential equations. When applied to a hierarchy of adaptively-refined meshes, geometric multigrid often reaches a point where further coarsening of the grid becomes impractical as individual subdomain sizes approach unity. At this point, a common solution in practice is to terminate coarsening at some level and use a Krylov subspace method, such as BICGSTAB, to reduce the residual by a fixed factor. This is called a `bottom solve'.
Each iteration of BICGSTAB requires multiple global reductions (MPI collectives), which involve communication between all processors. Because the number of BICGSTAB iterations required for convergence grows with problem size, and the time for each collective operation increases with machine scale, bottom solves can constitute a significant fraction of the overall multigrid solve time in large-scale applications.
In order to reduce this performance bottleneck, we have implemented, evaluated, and optimized a communication-avoiding 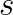 -step formulation of BICGSTAB (CA-BICGSTAB for short) as a high performance, distributed-memory bottom solver for geometric multigrid. This is the first time an
-step formulation of BICGSTAB (CA-BICGSTAB for short) as a high performance, distributed-memory bottom solver for geometric multigrid. This is the first time an 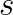 -step Krylov subspace method has been leveraged to improve multigrid bottom solver performance. The CA-BICGSTAB method is equivalent in exact arithmetic to the classical BICGSTAB method, but performs
-step Krylov subspace method has been leveraged to improve multigrid bottom solver performance. The CA-BICGSTAB method is equivalent in exact arithmetic to the classical BICGSTAB method, but performs 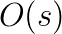 fewer global reductions over a fixed number of iterations at the cost of a constant factor of additional floating point operations and peer-to-peer messages. Furthermore, while increasing
fewer global reductions over a fixed number of iterations at the cost of a constant factor of additional floating point operations and peer-to-peer messages. Furthermore, while increasing 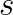 reduces the number of global collectives over a fixed number of iterations, it can also slow down convergence, requiring a greater number of total iterations to reduce the residual by the same factor. These tradeoffs between bandwidth, latency, and computation and between time per iteration and total iterations create an interesting design space to explore.
reduces the number of global collectives over a fixed number of iterations, it can also slow down convergence, requiring a greater number of total iterations to reduce the residual by the same factor. These tradeoffs between bandwidth, latency, and computation and between time per iteration and total iterations create an interesting design space to explore.
We used a synthetic benchmark to perform detailed performance analysis and demonstrate the benefits of CA-BICGSTAB. The best implementation was integrated into BoxLib, an AMR framework, in order to evaluate the benefits of the CA-BICGSTAB bottom solver in two applications: LMC, a low-Mach number combustion code, and Nyx, used for cosmological simulations. Using up to 32,768 cores on the Cray XE6 at NERSC, we obtained bottom solver speedups of up to 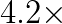 on synthetic problems and up to
on synthetic problems and up to 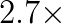 in real applications with parameter
in real applications with parameter 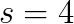 . This improvement resulted in up to a
. This improvement resulted in up to a 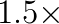 speedup in the overall geometric multigrid solve in real applications.
speedup in the overall geometric multigrid solve in real applications.
Piyush Sao (Georgia Institute of Technology), Richard Vuduc (Georgia Institute of Technology)
We show how to use the idea of self-stabilization, which originates in work by Dijkstra (1974) for problems in distributed control, to make fault-tolerant iterative solvers. At a high level, a self-stabilizing system is one that, starting from an arbitrary state (valid or invalid), reaches a valid state within a finite number of steps. This property imbues the system with a natural means of tolerating soft faults.
Our basic recipe for applying self-stabilization to numerical algorithm design is roughly as follows. First, we regard the execution of a given solver algorithm as the “system”. Its state consists of some or all of the variables that would be needed to continue its execution. Then, we identify a condition that must hold at each iteration for the solver to converge. When the condition holds, the solver is in a “valid” state; otherwise, it is in an invalid state. Finally, we augment the solver algorithm with an explicit mechanism that will bring it from an invalid state to a valid one within a guaranteed finite number of iterations. Importantly, the mechanism is designed so that the solver algorithm need not detect a fault explicitly. Rather, it is designed to cause a transition from an invalid to valid state automatically.
We have thus far devised two proof-of-concept self-stabilizing iterative linear solvers. One is a self-stabilized variant of steepest descent (SD) and the other is a variant of the conjugate gradient (CG) method. Our self-stabilized versions of SD and CG do require small amounts of fault-detection, e.g., we may check only for NaNs and infinities. Otherwise, under specific assumptions on the type and rates of transient soft faults, we can show formally that our modified solvers are self-stabilizing.
To get an idea of how this process works, consider the case of CG. Recall that CG constructs A-orthogonal search directions that span a Krylov subspace. In each iteration, it updates the solution estimate by taking a step of optimal size in the computed search direction. A fault, when it occurs, can
Our self-stabilized CG, through a periodic correction scheme we have devised, enforces the correctness of the problem being solved and restores certain local optimality and orthogonality properties of the generated search directions and residuals. One can prove that maintaining these properties satisfies the Zoutendijk Condition, which allows the (modified) solver to converge asymptotically, even in the presence in faults, provided the correction mechanism is invoked “frequently enough.” And in the absence of any faults, our self-stabilized CG remains equivalent to CG up to roundoff error.
To illustrate the fault tolerance property of self-stabilized algorithms, we test our self-stabilized CG experimentally by analyzing its convergence and overhead for different types and rates of faults in selective reliability mode, where we assume a small fraction of computation can be done in guaranteed reliable mode. We present a theoretical analysis relating amount of reliable computation required, rate of faults and problem being solved
Beyond the specific findings for the case of self-stabilized CG we believe self-stabilization has promise to become a useful tool for constructing resilient solvers more generally.
James Elliott (Sandia National Laboratories), Mark Hoemmen (Sandia National Laboratories ), Frank Mueller (North Carolina State University)
Much resilience research has focused on tolerating parallel process failures, either by improving checkpoint / restart performance, or introducing process replication. This matters because large-scale computers experience frequent single-process failures. However, it excludes the increasing likelihood of hardware anomalies which do not cause process failure. Even one incorrect arithmetic operation or memory corruption may cause incorrect results or increase run time, with no notification from the system. We refer to this class of faults as silent data corruption (SDC). Increasing parallelism and decreasing transistor feature sizes will make it harder to catch and correct SDC in hardware. Hardware detection and correction increase power from double-digit percentages to over twice as much. The largest parallel computers already have tight power limits, which will only get tighter. Thus, future extreme-scale systems may expose some SDC to applications. This will shift some burden to algorithms: either to detect and correct SDC, or absorb its effects and get the correct solution regardless.
This motivates our work on understanding how iterative linear solvers and preconditioners behave given SDC, and improving their resilience. We have yet to see a need for developing entirely new numerical methods. Rather, we find that hardening existing algorithms by careful introduction of more robust numerical techniques and invariant checks goes a long way. We advocate combining numerical analysis and systems approaches to do so.
Understanding algorithms' behavior in the presence of SDC calls for a new approach to fault models and experiments. Most SDC injection experiments randomly flip memory bits in running applications. However, this only shows average-case behavior for a particular subset of faults, based on an artificial hardware model. Algorithm developers need to understand worst-case behavior, and reason at an algorithmic level with the higher-level data types they actually use. Also, we know so little about how SDC may manifest in future hardware, that it seems premature to draw conclusions about the average case.
We argue instead that numerical algorithms can benefit from a numerical unreliability fault model, where faults manifest as unbounded perturbations to floating-point data. This favors targeted experiments that inject one or few faults in key parts of an algorithm, giving insight into the algorithm's response. It lets us extend lessons learned in rounding error analysis to the unbounded fault case. Furthermore, it leads to a resilience approach we call the skeptical programmer. Inexpensive checks of algorithm-specific invariants can exclude large errors in intermediate quantities. This bounds any remaining errors, making it easier to converge through them. While this requires algorithm-specific analysis, it identifies algorithms that naturally keep intermediate quantities bounded. These invariants also help detect programmer error. A healthy skepticism about subroutines' correctness makes sense even with perfectly reliable hardware, especially since modern applications may have millions of lines of code and rely on many third-party libraries.
Skepticism about intermediate results does not suffice for correctness despite SDC. This calls for a selective reliability programming model that lets us choose parts of an algorithm that we insist be correct. We combine selective reliability and skepticism about intermediate results to make iterative linear solvers reliable despite unbounded faults. This relies on an inner-outer solver approach, which does most of its work in the unreliable inner solver, that in turn preconditions the reliable outer solver. Using a flexible Krylov method for the latter absorbs inner faults. Our experiments illustrate this approach in parallel with different kinds of preconditioners in inner solves.
Jed Brown (Argonne National Laboratory), Mark Adams (Lawrence Berkeley National Laboratory), Dave May (ETH Zurich), Matthew Knepley (University of Chicago)
An interpretation of the full approximation scheme (FAS) multigrid method identifies a "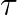 -correction" that represents the incremental influence of the fine grid on the coarse grid. This influence is robust to long-wavelength perturbations to the problem, allowing reuse between successive nonlinear iterations, time steps, or solves. For non-smooth problems such as brittle failure and contact, this permits fine grids to be skipped in regions away from the active nonlinearity. This technique provides benefits similar to adaptive mesh refinement, but is more general because the problem can have arbitrary fine-scale microstructure. We introduce the new method and present numerical results in the context of long-term lithosphere applications.
-correction" that represents the incremental influence of the fine grid on the coarse grid. This influence is robust to long-wavelength perturbations to the problem, allowing reuse between successive nonlinear iterations, time steps, or solves. For non-smooth problems such as brittle failure and contact, this permits fine grids to be skipped in regions away from the active nonlinearity. This technique provides benefits similar to adaptive mesh refinement, but is more general because the problem can have arbitrary fine-scale microstructure. We introduce the new method and present numerical results in the context of long-term lithosphere applications.
Jack Poulson (Georgia Institute of Technology), Greg Henry
Evaluating the norm of a resolvent over a window in the complex plane provides an illuminating generalization of a scatter-plot of eigenvalues and is of obvious interest for analyzing preconditioners. Unfortunately the common perception is that such a computation is embarrassingly parallel, and so little effort has been expended towards reproducing the functionality of the premier tool for pseudospectral computation, EigTool (Wright et al.), for distributed-memory architectures in order to enable the analysis of matrices too large for workstations.
This talk introduces several high-performance variations of Lui's triangularization followed by inverse iteration approach which involve parallel reduction to (quasi-)triangular or Hessenberg form followed by interleaved Implicitly Restarted Arnoldi iterations driven by multi-shift (quasi-)triangular or Hessenberg solves with many right-hand sides. Since multi-shift (quasi-)triangular solves can achieve a very high percentage of peak performance on both sequential and parallel architectures, such an approach both improves the efficiency of sequential pseudospectral computations and provides a high-performance distributed-memory scheme. Results from recent implementations within Elemental (P. et al.) will be presented for a variety of large dense matrices and practical convergence-monitoring schemes will be discussed.
Frederic Legoll (ENPC)
The Multiscale Finite Element Method (MsFEM) is a popular Finite Element type approximation method for multiscale elliptic PDEs. In contrast to standard finite element methods, the basis functions that are used to generate the MsFEM approximation space are specifically adapted to the problem at hand. They are precomputed solutions (in an offline stage) to some appropriate local problems, set on coarse finite elements. Next, the online stage consists in using the space generated by these basis functions (the dimension of which is limited) to build a Galerkin approximation of the problem of interest.
Many tracks, each of them leading to a specific variant of the MsFEM approach, have been proposed in the literature to precisely define these basis functions. In this work, we introduce a specific variant, inspired by the classical work of Crouzeix and Raviart, where the continuity of the solution across the edges of the mesh is enforced only in a weak sense. This variant is particularly interesting for problems set on perforated media, where inclusions are not periodically located. The accuracy of the numerical solution is then extremely sensitive to the boundary conditions set on the MsFEM basis functions. The Crouzeix-Raviart type approach we introduce proves to be very flexible and efficient.
Time permitting, we will also discuss a shape optimization problem for multiscale materials, which also leads to expensive offline computations in order to make the online optimization procedure affordable.
Jakub Šístek (Academy of Sciences of the Czech Republic), Bedřich Sousedík (University of Southern California), Jan Mandel (University of Colorado Denver)
In the first part of the talk, components of the Balancing Domain Decomposition based on Constraints (BDDC) method will be recalled. The method solves large sparse systems of linear equations resulting from discretisation of PDEs. The problem on the interface among subdomains is solved by the preconditioned conjugate gradient method, while one step of BDDC serves as the preconditioner.
In the second part of the talk, the algorithm of Adaptive-Multilevel BDDC will be described. It is based on a combination of two extensions of the standard BDDC method: The Adaptive BDDC, which aims at problems with severe numerical difficulties, generates constraints based on prior analysis of the problem and eliminates the worst modes from the space of admissible functions. Generalised eigenvalue problems are solved at each face between two subdomains, and the eigenvectors corresponding to a few largest eigenvalues are used for construction of the coarse space. The Multilevel BDDC is a recursive application of the BDDC method to successive coarse problems aiming at very large problems solved using thousands of compute cores. Finally, the parallel implementation of these concepts within our open-source BDDCML package will be presented. Performance of the solver is analysed on several benchmark and engineering problems, and main issues with an efficient implementation of both Adaptive and Multilevel extensions will be discussed.
Sanja Singer (University of Zagreb), Vedran Novakovic (University of Zagreb), Sasa Singer (University of Zagreb),
The generalized eigenvalue problem is of significant practical importance, especially in structural engineering where it arises as the vibration and buckling problems.
The Falk–Langemeyer method could be a method of choice for parallel solving of a definite generalized eigenvalue problem 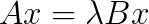 , where
, where 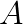 and
and 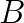 are Hermitian, and the pair is definite, i.e., there exist constants
are Hermitian, and the pair is definite, i.e., there exist constants 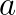 and
and 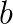 such that
such that 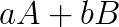 is positive definite.
is positive definite.
In addition, if both 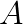 and
and 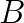 are positive definite, after a two-sided scaling with a diagonal matrix
are positive definite, after a two-sided scaling with a diagonal matrix  (this step is not necessary) and the Cholesky factorization of
(this step is not necessary) and the Cholesky factorization of 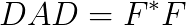 and
and 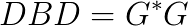 , the problem can be seen as the computation of the generalized singular value decomposition SVD of the Cholesky factors
, the problem can be seen as the computation of the generalized singular value decomposition SVD of the Cholesky factors 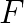 and
and 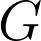 .
.
Here we present how to parallelize the Falk–Langemeyer method, by using a technique similar as in the parallelization of the one-sided Jacobi method for the SVD of a single matrix. By appropriate blocking of the method, an almost ideal load balancing between all available processors is obtained. A similar blocking technique, now on a processor level, can be used to exploit local cache memory to further speed up the process.
Neven Krajina (University of Zagreb)
In his dissertation, Pietzsch described a one-sided algorithm for diagonalization of skew-symmetric matrices which calculates the eigenvalues to high relative accuracy by using only real arithmetic. While there are algorithms for the same purpose, like QR method of Ward and Gray or Jacobi-like method of Paardekooper, they compute the eigenvalues of a skew-symmetric matrix 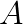 up to an absolute error bound of
up to an absolute error bound of 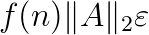 , where
, where 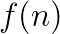 is some slowly growing function of the matrix order
is some slowly growing function of the matrix order 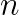 and
and 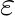 is the machine precision. Thus, eigenvalues of larger modulus are computed with high relative accuracy, while the smaller ones may not be relatively accurate at all. On the other hand, we can also reduce our matrix to tridiagonal skew-symmetric matrix and compute the eigenvalues by the bidiagonal QR method (without shifts) with high relative accuracy. Although Pietzsch method has the merit of accuracy, its disadvantage, as with other Jacobi-like methods, is speed, since algorithms of this class are known to be quite slow despite their quadratic convergence.
is the machine precision. Thus, eigenvalues of larger modulus are computed with high relative accuracy, while the smaller ones may not be relatively accurate at all. On the other hand, we can also reduce our matrix to tridiagonal skew-symmetric matrix and compute the eigenvalues by the bidiagonal QR method (without shifts) with high relative accuracy. Although Pietzsch method has the merit of accuracy, its disadvantage, as with other Jacobi-like methods, is speed, since algorithms of this class are known to be quite slow despite their quadratic convergence.
The algorithm can be split into two main parts: first we decompose a skew-symmetric matrix 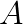 by a Cholesky-like algorithm of Bunch into
by a Cholesky-like algorithm of Bunch into 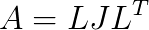 , where
, where 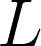 is a lower-triangular and
is a lower-triangular and 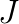 is a block diagonal matrix consisting of
is a block diagonal matrix consisting of 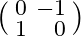 blocks. In the second part, we orthogonalize columns of matrix
blocks. In the second part, we orthogonalize columns of matrix 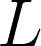 using symplectic transformations.
using symplectic transformations.
In this talk, we describe implementation of the above-mentioned method on graphic processing units. While retaining the same accuracy, our implementation shows substantial speedup in comparison to sequential algorithm.
Martin Bečka (Slovak Academy of Sciences), Gabriel Okša (Slovak Academy of Sciences), Marian Vajteršic (University of Salzburg)
Fast and accurate one-sided Jacobi SVD dense routine (by Drmac and Veselic) is a part of LAPACK from version 3.2. Beside high accuracy, it offers performance comparable to xGESVD. Although this serial algorithm is not easily parallelizable, some of its ideas, together with a dynamic ordering of parallel tasks and a suitable blocking data strategy lead to the algorithm competitive to PxGESVD of ScaLAPACK.
The matrix is logically distributed by block columns, where columns of each block are part of one orthogonal basis of a subspace participating in the orthogonalization iteration process. The dynamic ordering for orthogonalization of subspaces significantly reduces the number of parallel iterations of the algorithm. When l denotes the number of subspaces, then l/2 of them can be orthogonalized in parallel on p=l/2 processors. Breaking this relation and choosing l = p/k, we come to a reduction of iteration steps, as well as to an improvement of scalability of the whole algorithm. Computational experiments show, that this one-sided block-Jacobi algorithm is comparable to PxGESVD; it runs even faster for smaller values of p.
Yusaku Yamamoto (The University of Electro-Communications), Lang Zhang, Shuhei Kudo
Eigenvalue problem of a real symmetric matrix, 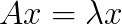 , is an important problem that has applications in quantum chemistry, electronic structure calculation and statistical calculation. In this study, we deal with the problem of computing all the eigenvalues and eigenvectors of a symmetric matrix
, is an important problem that has applications in quantum chemistry, electronic structure calculation and statistical calculation. In this study, we deal with the problem of computing all the eigenvalues and eigenvectors of a symmetric matrix 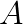 on a shared-memory parallel computer.
on a shared-memory parallel computer.
The standard method for the symmetric eigenvalue problem is based on tri-diagonalziation of the coefficient matrix. In fact, LAPACK, which is one of the standard linear algebra libraries, also adopts this approach. However, the algorithm of tri-diagonalziation is complicated and its parallel granularity is small. Due to this, when solving a small-sized problem, the overhead of communication and synchronization between processors becomes dominant and the performance is saturated with a small number of processors.
In this talk, we focus on the block-Jacobi algorithm for solving the symmetric eigenvalue problem, which is a generalization of the well known Jacobi algorithm. It works on a matrix partitioned into small blocks and tries to diagonalize the matrix by eliminating the off-diagonal blocks by orthogonal transformations. Although this algorithm requires much more work than the tri-diagonalziation based algorithm, it has simpler computational patterns and larger parallel granularity. Thanks to these features, the algorithm is easier to optimize on modern high performance processors. Moreover, it is expected to attain better scalability for small-size problems because the overhead of inter-processor communication and synchronization is smaller.
Based on this idea, we developed an eigenvalue solver based on the block-Jacobi algorithm for a shared-memory parallel computer. In the previous parallel implementations of the block Jacobi method, the cyclic block-Jacobi method, which eliminates the off-diagonal blocks in a pre-determined order, has been mainly used. Though this method is easier to parallelize, its convergence is relatively slow. For this reason, we chose to use the classical block-Jacobi method, which eliminates the off-diagonal block with the largest norm at each step. This method generally converges faster than the cyclic block-Jacobi method. To parallelize this method, it is necessary to find the set of off-diagonal blocks that can be eliminated in parallel and whose sum of norms is as large as possible. We can find such a set by using the idea of maximum weight matching from graph theory. In our algorithm, we find a near-maximum weight matching by using a greedy algorithm. Based on a theoretical analysis, our method is shown to have excellent properties such as global convergence and locally quadratic convergence.
We implemented our algorithm using OpenMP and evaluated its performance on the Intel Xeon processor with 6 cores (12 threads). When solving an eigenvalue problem of a 3,000 by 3,000 matrix, the parallel speedup was 3.8 with 6 cores. When compared with the LAPACK, which uses the tri-diagonalization based algorithm, our algorithm was slower, but in terms of the parallel speedup, our algorithm was superior. Also, when the input matrix is close to diagonal, the convergence of our algorithm was improved. From these results, we expect that our algorithm can be superior to the tri-diagonalization based one when solving a number of eigenvalue problems whose coefficient matrices are slightly different from each other using a many-core processor.
Andreas Schäfer (University of Erlangen-Nuremberg), Dietmar Fey (University of Erlangen-Nuremberg)
We present an advanced latency hiding algorithm for tightly coupled, iterative numerical methods. As a first, it combines overlapping calculation and communication with wide halos which limit communication to every k-th step. This approach trades computational overhead for an improved decoupling of neighboring nodes. Thereby, it can effectively hide network latencies that exceed the compute time for a single time step. It is most beneficial for strong scaling setups and accelerator-equipped systems. We provide insights into how this algorithm can be expanded to improve fault resilience.
George Bosilca (University of Tennessee), Thomas Herault (University of Paris-Sud), Aurelien Bouteiller (University of Tennessee)
Time-to-completion and energetic costs are some of the units used to measure the impact of fault tolerance on production parallel applications. These costs have an extremely complex definition and involve many parameters. This talk will cover some of the most prominent parameters for traditional fault tolerance approaches, and describe a toolbox and it’s corresponding API. This extension to MPI is called User Level Failure Mitigation, and allows developers to design and implement the minimal and most efficient fault tolerance model needed by their parallel applications.
Sebastien Cayrols (INRIA), Laura Grigori (INRIA), Sophie Moufawad (INRIA)
In this talk we discuss a communication avoiding ILU0 preconditioner for solving large linear systems of equations by using iterative Krylov subspace methods. Our preconditioner allows to compute and apply the ILU0 preconditioner with no communication, through ghosting some of the input data and performing redundant computation. To avoid communication, an alternating reordering algorithm is introduced for structured and well partitioned unstructured matrices, that requires the input matrix to be ordered by using a graph partitioning technique such as k-way or nested dissection. We present performance results of CA-ILU0 and compare it to classical ILU0, Block Jacobi and RAS preconditioners.
Dominik Göddeke (Technical University of Dortmund), Mirco Altenbernd (Technical University of Dortmund), Dirk Ribbrock (Technical University of Dortmund)
Hierarchical multigrid methods are widely recognised as the only (general) class of algorithms to solve large, sparse systems of equations in an asymptotically optimal and thus algorithmically scalable way. For a wide range of problems, they form the key building block that dominates runtime, in particular in combination with numerically powerful implicit approaches for nonstationary phenomena and Newton-type schemes to treat nonlinearities.
In this talk, we analyse and discuss the numerical behaviour of geometric finite-element multigrid solvers in the presence of hardware failures and incorrect computation: Events like the loss of entire compute nodes, bitflips in memory, or silent data corruption in arithmetic units are widely believed to become the rule rather than the exception. This is due to permanently increasing node counts at scale, in combination with chip complexity, transistor density, and tight energy constraints.
We first analyse the impact of small- and large-scale failures and faults, i.e., partial loss of iterates or auxiliary arrays, on the convergence behaviour of finite-element multigrid algorithms numerically. We demonstrate that as long as the input data (matrix and right hand side) are not affected, multigrid always converges to the correct solution.
We then introduce a minimal checkpointing scheme based on the inherent data compression within the multilevel representation. This approach, in combination with partial recovery, almost maintains the convergence rates of the fault-free case even in the presence of frequent failures. We analyse the numerical and computational trade-off between the size of the checkpoint information and the performance and convergence of the solver. Special emphasis is given to the effect of discontinuous jumps in the solution that appear when components are eliminated, or restored from old intermediate data.
Simplice Donfack (Università della Svizzera italiana ), Stanimire Tomov (University of Tennessee), Jack Dongarra (University of Tennessee), Olaf Schenk (Università della Svizzera italiana)
We present an efficient hybrid CPU/GPU approach that is portable, dynamically and efficiently balances the workload between the CPUs and the GPUs, and avoids data transfer bottlenecks that are frequently present in numerical algorithms. Our approach determines the amount of initial work to assign to the CPUs before the execution, and then dynamically balances workloads during the execution. Then, we present a theoretical model to guide the choice of the initial amount of work for the CPUs. The validation of our model allows our approach to self-adapt on any architecture using the manufacturer's characteristics of the underlying machine. We illustrate our method for the LU factorization. For this case, we show that the use of our approach combined with a communication avoiding LU algorithm is efficient. For example, our experiments on a 24 cores AMD opteron 6172 show that by adding one GPU (Tesla S2050) we accelerate LU up to 2.4 X compared to the corresponding routine in MKL using 24 cores. The comparisons with MAGMA also show significant improvements.
Nicholas Knight (University of California, Berkeley), James Demmel (University of California, Berkeley), Grey Ballard (University of California, Berkeley), Nicholas Knight (University of California, Berkeley), Edgar Solomonik (University of California, Berkeley)
Communication, i.e., data movement, typically dominates the algorithmic costs of computing the eigenvalues and eigenvectors of large, dense symmetric matrices. This observation motivated multistep approaches for tridiagonalization, which perform more arithmetic operations than one-step approaches, but can asymptotically reduce communication.
We study multistep tridiagonalization on a distributed-memory parallel machine and propose several algorithmic enhancements that can asymptotically reduce communication compared to previous approaches. In the first step, when reducing a full matrix to band form, we apply the ideas of the tall-skinny QR algorithm and Householder reconstruction to minimize the number of interprocessor messages (along the critical path). In subsequent steps, when reducing a band matrix to one with narrower bandwidth, we extend Lang's one-step band tridiagonalization algorithm to a multistep approach, enabling a reduction in both messages and on-node data movement. For thicker bands, we propose a pipelined approach using a 2D block cyclic layout (compatible with ScaLAPACK's), where we agglomerate orthogonal updates across bulge chases; for thinner bands, we apply the idea of chasing multiple (consecutive) bulges, previously studied in shared-memory. In addition to asymptotically decreasing algorithmic costs over a wide range of problem sizes, when the input data is so large that its storage consumes all but a constant fraction of the machine's memory capacity, our approach attains known lower bounds on both the number of words moved between processors and on the number of messages in which these words are sent (along the critical path). Moreover, our approach also benefits the sequential case, asymptotically reducing the number of words and messages moved between levels of the memory hierarchy, and, again, attaining lower bounds. We benchmark and compare our approach with previous works like ELPA to evaluate whether minimizing communication improves overall performance.
We also consider the limitations of our approach and discuss possible extensions. First, the tradeoffs of multistep approaches are much greater when eigenvectors are computed, due to the cost of back-transformation, i.e., applying the orthogonal transformations generated by the tridiagonalization steps. Our approach shows, perhaps surprisingly, that it can be beneficial to perform band reduction steps redundantly, on different subsets of processors, in order to reduce communication involved with the back-transformation. In contrast to previous approaches, which perform only one or two tridiagonalization steps in order to minimize the back-transformation costs, our results show that it can be worthwhile to perform more steps, even when eigenvectors are computed. In practice, we navigate the back-transformation tradeoffs with performance modeling and parameter tuning. Second, if more than a constant fraction of memory is unused, other approaches are needed to exploit this memory to further reduce communication and attain the (smaller) lower bounds that apply; we mention our ongoing work for this scenario. Third, we show how our approach extends to many other applications of multistep band reduction, like Hermitian tridiagonalization, bidiagonalization, and Hessenberg reduction.
Sheng Fang (University of Oxford), Raphael Hauser (University of Oxford)
A novel algorithm for leading part SVD computations of large scale dense matrices is proposed. The algorithm is well adapted to the novel computational architectures and satisfies the loosely coupled requirements(low synchronicity and low communication overheads). In contrast to randomized approaches that sample a subset of the data matrix, our method looks at all the data and works well even in cases where the former algorithms fail. We will start with a geometric motivation of our approach and a discussion of how it differs from other approaches. The convergence analysis is split into the derivation of bounds on the local error occurring at individual nodes, and bounds on the global error accumulation. Several variants of the algorithm will be compared, and numerical experiments and applications in matrix optimization problems will also be discussed.
Ren Xiaoguang (National University of Defense Technology)
With the development of the electronic technology, the processors count in a supercomputer reaches million scale. However, the processes scale of a application is limited to several thousands, and the scalability face a bottleneck from several aspects, including I/O, communication, cache access, etc. In this paper, we focus on the communication bottleneck to the scalability of linear algebraic equation solving. We take preconditioned conjugate gradient (PCG) as an example, and analysis the feathers of the communication operations in the process of PCG solver. We find that reduce communication is the most critical issue for the scalability of the parallel iterative method for linear algebraic equation solve. We propose a local residual error optimization scheme to eliminate part of the reduce communication operations in the parallel iterative method, and improve the scalability of the parallel iterative method. Experimental results on the Tianhe-2 supercomputer demonstrate that our optimization scheme can achieve a much signally effect for the scalability of the linear algebraic equation solve.
Maya Neytcheva (Uppsala University), Ali Dorostkar (Uppsala University), Dimitar Lukarski (Uppsala University), Björn Lund (Uppsala University), Yvan Notay (Université libre de Bruxelles), Peter Schmidt (Uppsala University)
We consider large scale computer simulations of the so-called Glacial Isostatic Adjustment model, describing the submerge or elevation of the Earth surface as a response to redistribution of mass due to alternating glaciation and deglaciation periods.
We consider a 2D model that is often used in the geophysics community, where self-gravitation is excluded. Due to the latter, the Earth is modelled as incompressible. The governing equations are 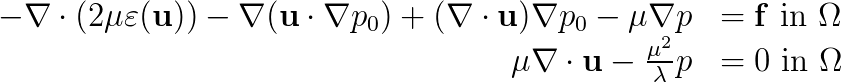 where the coefficients
where the coefficients 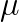 ,
, 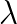 are the Lamé coefficients,
are the Lamé coefficients, 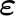 is the strain tensor,
is the strain tensor, 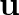 is the displacement vector,
is the displacement vector, 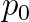 is the so-called pre-stress,
is the so-called pre-stress,  is a body force and
is a body force and 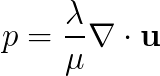 is the so-called kinematic pressure, introduced in order to be able to simulate fully incompressible materials, for which
is the so-called kinematic pressure, introduced in order to be able to simulate fully incompressible materials, for which 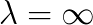 .
.
The model is discretized using the finite element method. It gives raise to algebraic systems of equations that are large, sparse, nonsymmetric and indefinite, and have the following saddle point structure, 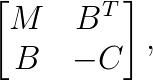 where the pivot block
where the pivot block 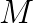 is nonsymmetric.
is nonsymmetric.
These linear systems are solved using Krylov subspace iteration methods and a block preconditioner of block-triangular form, that requires inner-outer iterations. Algebraic multigrid is used as an inner solver. The efficiency of solving one system of the above type is crucial as it will be embedded in a time-evolution procedure, where systems with matrices with similar characteristics have to be solved repeatedly.
The simulations are performed using toolboxes from publicly available software packages - deal.ii, Trilinos, Paralution and AGMG. The numerical experiments are performed using OpenMP-type parallelism on multicore CPU systems as well as on GPU. We present performance results in terms of numerical and computational efficiency, number of iterations and execution time, and compare the timing results against a sparse direct solver from a commercial finite element package.
References:
deal.ii: http://www.dealii.org
Trilinos: http://trilinos.sandia.gov/
Paralution: http://www.paralution.com
AGMG: http://homepages.ulb.ac.be/ ynotay/AGMG/
Markus Blatt (HPC-Simulation-Software & Services)
We present a parallel algebraic (AMG) multigrid method based on on-smoothed aggregation for preconditioning the elliptic problem 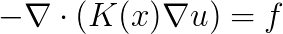 on bounded domains
on bounded domains 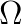 .
.
Our method is robust for highly variable or even discontinuous coefficients 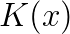 . It is developed for massively parallel supercomputers with a low amount of main memory per core. Due to a greedy heuristic used for the coarsening the method has a low memory footprint and allows for scalable subsurface flow simulations with up to 150 billion unknowns on nearly 300 thousand cores.
. It is developed for massively parallel supercomputers with a low amount of main memory per core. Due to a greedy heuristic used for the coarsening the method has a low memory footprint and allows for scalable subsurface flow simulations with up to 150 billion unknowns on nearly 300 thousand cores.
The implementation is available as open source within the "Distributed and Unified Numerics Environment" (DUNE).
Seiji Fujino (Kyushu University), Chiaki Itou
We want to solve a linear system of equations as 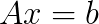 , where
, where 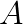 is a sparse real
is a sparse real 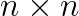 matrix,
matrix, 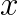 and
and 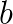 are solution and right-hand side vectors of order
are solution and right-hand side vectors of order 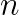 , respectively. We consider to split the matrix
, respectively. We consider to split the matrix 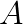 as
as 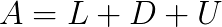 , where
, where 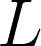 ,
, 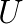 and
and  denote lower, upper triangular matrices and diagonal matrix, respectively. Moreover, we treat with preconditioned linear systems as
denote lower, upper triangular matrices and diagonal matrix, respectively. Moreover, we treat with preconditioned linear systems as 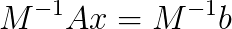 , where
, where 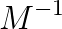 means a preconditioner matrix.
means a preconditioner matrix.
As well known, Eisenstat trick of Symmetric SOR is an efficient preconditioning. In this algorithm, 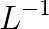 and
and 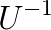 as splits of coefficient matrix
as splits of coefficient matrix 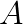 are computed in place of incomplete factorization of matrix
are computed in place of incomplete factorization of matrix 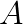 . Accordingly it does not need so much computational time in multiplication of preconditioner
. Accordingly it does not need so much computational time in multiplication of preconditioner 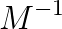 and matrix
and matrix 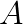 . However, it is not suited to parallel computation. In particular, preconditioning of Eisenstat SSOR is not executed efficiently on parallel computers with distributed memory.
. However, it is not suited to parallel computation. In particular, preconditioning of Eisenstat SSOR is not executed efficiently on parallel computers with distributed memory.
In our talk, we will propose Cache-Cache balancing technique for Eisenstat type of preconditioning on parallel computers with distributed memory. “ Cache-Cache” in French means “ hide and seek” in English. The nonzero entries of 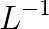 once hidden for parallelism are found in computation of
once hidden for parallelism are found in computation of 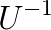 for balancing the original matrix
for balancing the original matrix 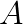 . Through numerical experiments, we will make clear that the proposed Cache-Cache balancing technique for parallelism outperforms some conventional preconditionings.
. Through numerical experiments, we will make clear that the proposed Cache-Cache balancing technique for parallelism outperforms some conventional preconditionings.
Hartwig Anzt (University of Tennessee), Edmond Chow (Georgia Institute of Technology), Jack Dongarra (University of Tennessee)
Based on the premise that preconditioners needed for scientific computing are not only required to be robust in the numerical sense, but also scalable for up to thousands of light-weight cores, the recently proposed approach of computing an ILU factorization iteratively is a milestone in the concept of algorithms for Exascale computing. While ILU preconditioners, often providing appealing convergence improvement to iterative methods like Krylov subspace solvers, are among the most popular methods, their inherently sequential factorization is often daunting. Although improvement strategies like level-scheduling or multi-color ordering render some parallelism, the factorization often remains an expensive building block, especially when targeting large-scale systems. The iterative ILU computation offers an efficient workaround, as it allows for not only fine-grained parallelism, but also excessive asynchronism in the iterative component updates providing the algorithmic characteristics needed for future HPC systems: - The algorithm allows for scaling to any core count, while only the number of nonzero elements in the factorization sets an efficiency-bound. - Communication latencies are of minor impact, and hierarchical distribution of the data allows for reduction of the communication volume. - The asynchronism implies algorithmic error-resilience, as hardware-failures as well as soft errors neither result in the breakdown, nor in the need for restart. This intrinsic fault-tolerance also removes the need for checkpointing strategies or error-resilient communication, both detrimental to performance. At the same time, the operation characteristics of streaming processors like GPUs promote inherently asynchronous algorithms. While implementing linear algebra routines usually requires careful synchronization, the tolerance for asynchronism makes the iterative ILU factorization an ideal candidate for efficient usage of the computing power provided by GPUs. The increasing number of high-performance computing platforms featuring coprocessors like GPUs results in a strong demand for suitable algorithms. In this paper we review the iterative approach of computing the ILU factorization, and the potential of its GPU implementations. We evaluate different approaches that result in either totally asynchronous iteration, or algorithms in which subsets have a pre-defined update order, with iterating asynchronously between the subsets. For those block-asynchronous strategies, the convergence is obviously ensured as they arise as a special case of asynchronous iteration, their performance might benefit from appealing cache reusage on the GPUs. In this case, the granularity of the asynchronism is sallied to a block level, but in contrast to classical block-asynchronous methods, where blocks are usually formed out of adjacent vector components, this approach blocks matrix entries that are adjacent in memory, but not necessarily in the matrix. We compare the performance characteristics of the implementations featuring different asynchronism granularity for several matrix storage formats and matrix sparsity pattern. We also investigate the impact of the asynchronism. Using the shift representing the age of the oldest component used in an update as a control parameter we analyze the trade-off between performance and convergence rate. Careful inspection reveals that the performance-optimal choice of the shift depends primarily on the hardware characteristics, while the properties of the matrix have a minor impact. Although the potential of the asynchronous ILU computation primarily pays off when targeting large-scale problems, we also include a brief comparison against direct ILU factorizations for problems of moderate size.
Lukasz Szustak (Częstochowa University of Technology), Krzysztof Rojek (Częstochowa University of Technology), Roman Wyrzykowski (Czestochowa University of Technology), Pawel Gepner (Intel Corporation)
The multidimensional positive definite advection transport algorithm (MPDATA) belongs to the group of nonoscillatory forward in time algorithms, and performs a sequence of stencil computations. MPDATA is one of the major parts of the dynamic core of the EULAG geophysical model.
The Intel Xeon Phi coprocessor is the first product based on the Intel Many Integrated Core (Intel MIC) architecture. This architecture offers notable performance advantages over traditional processors, and supports practically the same traditional parallel programming model. Intel MIC architecture combines more than 50 cores (200 threads) within a single chip, it has at least 25 MB aggregated L2 cache and 6 GB of on-board memory. The Intel Phi coprocessor is delivered in form factor of a PCIe device.
In this work, we outline an approach to adaptation of the 3D MPDATA algorithm to the Intel MIC architecture. This approach is based on combination of loop tiling and loop fusion techniques, and allows us to ease memory and communication bounds and better exploit the theoretical floating point efficiency of target computing platforms. The proposed approach is than extended on clusters with Intel Xeon Phi coprocessors, using a mixture of MPI and OpenMP programming standards. For this aim, we use a hierarchical decomposition of MPDATA, including level of cluster as well as distribution of computation across cores of Intel Xeon Phi. We discuss preliminary performance results achieved for cluster with Intel Xeon Phi 5120D.
Yves Ineichen (IBM Research - Zurich), Costas Bekas (IBM Research - Zurich), Alessandro Curioni (IBM Research - Zurich)
Over the years graph analytics has become a cornerstone for a wide variety of research areas and applications, and a respectable number of algorithms have been developed to extract knowledge from big and complex graphs. Unfortunately, the high complexity of these algorithms poses a severe restriction on the problem sizes. Indeed, in modern applications such as social or bio inspired networks, the demand to analyze larger and larger graphs now routinely range in the tens of millions and out-reaching to the billions in notable cases.
We believe that in the era of the big data regime accuracy has to be traded for algorithmic complexity and scalability to drive big data analytics. With this goal in mind we developed novel near linear (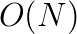 ) methods for graph analytics. In this talk we will focus on two algorithms: estimating subgraph centralities (measure for the importance of a node), and spectrograms (density of eigenvalues) of the adjacency matrix of the graph. On one hand we discuss the underlaying mathematical models relaying on matrix trace estimation techniques. On the other hand we discuss the exhibited parallelism on multiple levels in order to attain good parallel efficiency on a large number of processes. To that end we explore the scalability of the proposed algorithms with benchmarks on huge datasets, e.g. the graph of the European street network containing 51 million nodes and 108 million non-zeros. Due to the iterative behavior of the methods, a very good estimate can be computed in a matter of seconds.
) methods for graph analytics. In this talk we will focus on two algorithms: estimating subgraph centralities (measure for the importance of a node), and spectrograms (density of eigenvalues) of the adjacency matrix of the graph. On one hand we discuss the underlaying mathematical models relaying on matrix trace estimation techniques. On the other hand we discuss the exhibited parallelism on multiple levels in order to attain good parallel efficiency on a large number of processes. To that end we explore the scalability of the proposed algorithms with benchmarks on huge datasets, e.g. the graph of the European street network containing 51 million nodes and 108 million non-zeros. Due to the iterative behavior of the methods, a very good estimate can be computed in a matter of seconds.
Both analytics have an immediate impact on visualizing and exploring large graphs arising in many fields.
Vaclav Hapla (Technical University of Ostrava), Martin Cermak (Technical University of Ostrava), David Horak (Technical University of Ostrava), Alexandros Markopoulos (Technical University of Ostrava), Lubomir Riha (Technical University of Ostrava)
Discretization of most engineering problems, described by partial differential equations, leads to large sparse linear systems of equations. However, problems that involve variational inequalities, such as those describing the equilibrium of elastic bodies in mutual contact, can be more naturally expressed as quadratic programming problems (QPs). A QP takes the form
 where
where 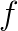 is a quadratic function of the form
is a quadratic function of the form 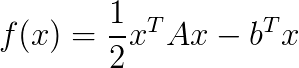 and
and 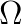 is a feasible set containg only
is a feasible set containg only 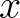 satisfying zero or more prescribed constraints of any of the following forms
\begin{align}
B_Ex &= c_E,
satisfying zero or more prescribed constraints of any of the following forms
\begin{align}
B_Ex &= c_E,
B_Ix &\leq c_I,
l \leq x &\leq u,
\end{align}
where
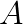
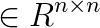 is the symmetric positive semidefinite Hessian matrix,
is the symmetric positive semidefinite Hessian matrix,
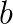
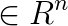 is the right hand side vector,
is the right hand side vector,
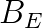
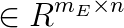 is the equality constraint matrix,
is the equality constraint matrix,
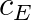
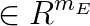 is the equality constraint right hand side vector,
is the equality constraint right hand side vector,
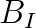
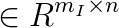 is the inequality constraint matrix,
is the inequality constraint matrix,
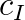
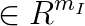 is the inequality constraint right hand side vector,
is the inequality constraint right hand side vector,
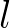
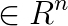 is the lower bound vector,
and
is the lower bound vector,
and 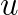
 is the upper bound vector.
is the upper bound vector.
We shall introduce here our emerging software stack PERMON. It makes use of theoretical results in advanced quadratic programming algorithms, discretization and domain decomposition methods, and is built on top of the respected PETSc framework for scalable scientific computing, providing parallel matrix algorithms and linear system solvers. The core solver layer of PERMON has arised from splitting the former FLLOP (FETI Light Layer on Top of PETSc) package into several modules: PermonDDM (aka FLLOP) library module for (the algebraical part of) domain decomposition methods (primarily those from FETI family), PermonQP library module for quadratic programming, and PermonAIF which is a pure C array based wrapper of PermonDDM and PermonQP useful for users wanting to take advantage of Permon in their software but do not understand/want/need object-oriented PETSc API. Other layer include application-specific solver modules such as PermonPlasticity, discretization tools such as PermonCube, interfaces allowing calling FLLOP from external discretization software such as libMesh or Elmer. We will present a snapshot of the current state and an outlook for near future.
Alberto Garcia-Robledo (CINVESTAV), Arturo Diaz-Perez (CINVESTAV), Guillermo Morales-Luna (CINVESTAV)
There exists a growing interest in the reconstruction of a variety of technological, sociological and biological phenomena using complex networks. The emerging “science of networks” has motivated a renewed interest in classical graph problems such as the efficient computing of shortest paths and breadth-first searches (BFS). These algorithms are the building blocks for a new set of applications related to the analysis of the structure of massive real-world networks.
All-Sources BFS (AS-BFS) is a highly recurrent kernel in complex network applications. It consists of performing as many full BFS traversals as the number of vertices of the network, each BFS starting from a different source vertex. AS-BFS is the core of wide variety of global and centrality metrics that allow us to evaluate global aspects of the topology of huge networks and to determine the importance of a particular vertex.
The massive size of the phenomena that complex networks model introduce large amounts of processing times that might be alleviated by exploiting modern hardware accelerators, such as GPUs and multicores. However, existing results accelerating BFS-related problems reveal the existing gap between complex network algorithms and current parallel architectures.
There is an useful duality between fundamental operations of linear algebra and graph traversals. For example, in [Qian et al. 2012] it is proposed a GPU approach that overcome the irregular data access patterns on graphs from Electronic Design Automation (EDA) applications by moving BFS to the realm of linear algebra using sparse matrix-vector multiplications (SpMVs). Sparse matrix operations provide a rich set of data-level parallelism, high arithmetic loads and clear data-access patterns, suggesting that an algebraic formulation of BFS can take advantage of the GPU data-parallel architecture.
Unfortunately, there is neither a systematic study on the algebraic BFS approach on non-EDA networks nor a study that compares the algebraic and visitor strategies. Is the algebraic approach adequate for accelerating measurements on complex networks? How they compare on graphs with different structure?
In this paper, we develop an experimental study of the algebraic AS-BFS on GPUs and multicores, by methodologically comparing the visitation and the algebraic approaches on complex networks. We experimented on a variety of synthetic regular, random, and scale-free networks, in order to reveal the impact of the network topology on the GPU and multicore performance and show the suitability of the algebraic AS-BFS for these architectures.
We experimented with sparse and dense graphs with varying diameter, degree distribution and edge density. In order to create graphs with the desired structure, we made use of the well-known Gilbert and Barabási-Albert random graph models, which create uncorrelated random graphs with Poisson and scale-free degree distribution, respectively.
We found that structural properties present in complex networks influence the performance of AS-BFS strategies in the following (decreasing) order of importance: (1) whether the graph is regular or non-regular, (2) whether the graph is scale-free or not, (3) and the graph density. We also found that even though the SpMV approach is not well suited for multicores, the GPU SpMV strategy can outperform the GPU visitor strategy on low-diameter graphs.
In addition, we show that CPUs and GPUs are suitable for complementary kinds of graphs, being GPUs better suited for random sparse graphs. The presented empirical results might be useful for the design of an hybrid network processing strategy that considers how the different algorithmic BFS approaches perform differently on networks with different structure.
Eric Darve (Stanford University)
In recent years there has been a resurgence in direct methods to solve linear systems. These methods can have many advantages compared to iterative solvers; in particular their accuracy and performance is less sensitive to the distribution of eigenvalues. However, they typically have a larger computational cost in cases where iterative solvers converge in few iterations. We will discuss a recent trend of methods that address this cost and can make these direct solvers competitive. Techniques involved include hierarchical matrices, hierarchically semi-separable matrices, fast multipole method, etc.
Wim Vanroose (University of Antwerp)
The main algorithmic components of a preconditioned Krylov method are the dot-product and the sparse-matrix vector product. On modern HPC hardware the performance of Preconditioned Krylov methods is severely limited due to two communication bottlenecks. First, each dot product has a large latency due to the involved synchronization and global reduction. Second, each sparse-matrix vector product suffers from the limited memory bandwidth because it does only a few floating point computations for each byte read from main memory. In this talk we discuss how Krylov methods can be redesigned to alleviate these two communication bottlenecks.
Eike Mueller (University of Bath), Robert Scheichl (University of Bath)
The continuous increase in model resolution in all areas of geophysical modeling requires the development of efficient and highly scalable solvers for very large elliptic PDEs. For example, implicit time stepping methods in weather and climate prediction require the solution of an equation for the atmospheric pressure correction at every time step and this is one of the computational bottlenecks of the model. The discretized linear system has around 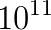 unknowns if the horizontal resolution is increased to around 1 kilometer in a global model run and weather forecasts can only be produced at operational time scales at this resolution if the PDE can be solved in a fraction of a second. Only solvers which are algorithmically scalable and can be efficiently parallelised on
unknowns if the horizontal resolution is increased to around 1 kilometer in a global model run and weather forecasts can only be produced at operational time scales at this resolution if the PDE can be solved in a fraction of a second. Only solvers which are algorithmically scalable and can be efficiently parallelised on 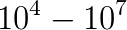 processor cores can deliver this performance. As the equation is solved in a thin spherical shell representing the earth's atmosphere, the solver has to be able to handle very strong vertical anisotropies; equations with a similar structure arise in many other areas in the earth sciences such as global ocean models, subsurface flow simulations and ice sheet models.
processor cores can deliver this performance. As the equation is solved in a thin spherical shell representing the earth's atmosphere, the solver has to be able to handle very strong vertical anisotropies; equations with a similar structure arise in many other areas in the earth sciences such as global ocean models, subsurface flow simulations and ice sheet models.
We compare the algorithmic performance and massively parallel scalability of different Krylov-subspace and multigrid solvers for the pressure correction equation in semi-implicit semi-Lagrangian time stepping for atmospheric models. We studied both general purpose AMG solvers from the DUNE (Heidelberg) and hypre (Lawrence Livermore Lab) libraries and developed a bespoke geometric multigrid preconditioner tailored to the geometry and anisotropic structure of the equation.
Based on the tensor-product multigrid approach first analysed by Boerm and Hiptmair [Numer. Algorithms, 26/3 (2001), 219-234] we implemented and optimised a highly efficient multigrid algorithm for equations with a strong grid aligned anisotropy. The solver is algorithmically optimal and scales to very large core counts both on CPU- and GPU architectures. To achieve optimal performance, it has to be implemented efficiently and exploit parallelism on different levels. As in any grid-based methods a particular challenge for memory bound applications is the small FLOP/bandwidth ratio on modern architectures such as GPUs (on a Kepler K20X GPU card 30 FLOPs can be executed in the time it takes to load a floating point number from memory). To minimise global memory transfer we developed a matrix-free implementation which recalculates the local matrix stencil on the fly instead of loading it from global memory. We demonstrate that this leads to significantly better performance than matrix-explicit implementations based on standard CUDA libraries; other techniques such as kernel fusion further improve the single-GPU performance. We parallelised the method across multiple GPUs with the Generic Communication Library (GCL) developed at CSCS Switzerland.
The exact nature of future HPC systems is still undecided and it is important to investigate scalability and performance both on more traditional CPU clusters and on novel architectures such as GPUs. We demonstrate the massively parallel scalability of our solvers on up to 65536 cores of the CPU based HECToR Cray cluster and present scalability studies on up to 16384 GPUs (corresponding to 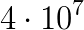 individual cores) of the Titan supercomputer (#2 www.top500.org, Nov 2013) and the EMERALD cluster. The largest system, we studied has
individual cores) of the Titan supercomputer (#2 www.top500.org, Nov 2013) and the EMERALD cluster. The largest system, we studied has 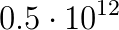 unknowns and can be solved in one second with our matrix-free tensor-product multigrid solver on Titan. On this machine our implementation achieves a peak performance of up to 0.8 petaFLOPs per second and it can utilise between 25% and 50% of the global memory bandwidth, which is a sizeable fraction for a memory bound application.
unknowns and can be solved in one second with our matrix-free tensor-product multigrid solver on Titan. On this machine our implementation achieves a peak performance of up to 0.8 petaFLOPs per second and it can utilise between 25% and 50% of the global memory bandwidth, which is a sizeable fraction for a memory bound application.
Fred Wubs (University of Groningen), Weiyan Song and Jonas Thies (German Aerospace Center)
Many flow problems deal with transport of matter and/or heat. This constitutes a challenging multiphysics problem if the transported entity also influences the flow. From a computing efficiency view point, it is best to treat the associated equations in a coupled manner [5]. Employing a domain decomposition approach, all the unknowns related to one domain should be in the memory of the node which treats that part. Moreover, communication should be avoided as much as possible during the construction of the right-hand side, the construction of the Jacobian matrix and the solution process. Along this line we developed a finite volume package FVM and a solver HYMLS, both based on elements of the EPETRA-package (available within Trilinos (see http://trilinos.sandia.gov/)).
Our implementation is matrix oriented instead of function oriented. Before computation we compute and store all stencils needed in the code. From the nonlinear terms, which are here bilinear forms, we store the constituting operators also in the form of stencils. The Jacobian matrix and the right-hand side are now constructed from products of stencils and vectors. To solve the nonlinear equations we use the NOX package with our in house developed package HYMLS to solve the systems.
HYMLS is a linear system solver for steady state incompressible Navier-Stokes equations coupled to transport equations in 2 and 3D [1,2,3]. Recently, we constructed a multilevel variant of it, which makes it possible to solve 3D problems of over 10 million unknowns quickly on a parallel computer. The behavior of the method is very much like that of multigrid methods. The solver is very robust. For the problem described in [4], it allowed a quick increase in the Reynolds number to get into the interesting region around Re=2000. Here we will show the performance of the method on the Rayleigh-Bénard convection in a cube, with six no-slip walls [6].
To study the stability of the solutions we determine the eigenvalues using the ANASAZI-package, which contains a generalized version of the Arnoldi method. Also here we employ HYMLS to solve the linear systems that result from a Cayley transform of the generalized eigenvalue problem. In the talk we will give a more detailed explanation of the used algorithms and their performance.
References
 factorization of F-type saddle point matrices. IMA Journal of Numerical Analysis, 29(1), 208-234, 2009.
factorization of F-type saddle point matrices. IMA Journal of Numerical Analysis, 29(1), 208-234, 2009.Thomas Huckle (Technische Universität München), Jürgen Bräckle (Technische Universität München)
We consider the Jacobi Davidson method for computing eigenvalues for Plasma Physic problems in a parallel environment. The linear system that has to be solved in each iteration step has to be preconditioned in order to ensure fast convergence. The preconditioner should lead to fast convergence and allow efficient parallel computations. Similar to BFSAI (block factorized sparse approximate inverses) we combine two preconditioning methods, a sparse approximate inverse and an approximate direct preconditioner like e.g. Block Jacobi. We test and compare different combinations applied on the Plasma Turbulence Code Gene.
Matthias Bolten (University of Wuppertal)
While multigrid methods have shown very good scalability even on the largest supercomputers available, the ratio of computation and communication is rather low, thus affecting the efficiency especially on modern computer architectures like GPUs or accelerators in general. One way to overcome this is by using more efficient smoothers in the sense that they use less communication steps for the same amount of error reduction in the rough components. This not only improves the convergence rate per V-cycle, it also allows for more aggressive coarsening and opens room for improving multigrid performance on different hardware architectures. One option for more efficient smoothers in the sense above are domain decomposition-like smoothers that invert small local subdomains, possibly including overlap, like in standard domain decomposition methods. The price for these highly efficient smoothers is their computational cost that is larger than that of a point smoother. Nevertheless, modern computer architectures benefit from the higher locality of the operations required, yielding a reduced time to solution.
In the talk we will present the idea and numerical results of the obtained methods. The numerical experiments show that the higher number of arithmetic operations is not visible, as the computation on the blocks is local and thus much better suited to the needs of modern parallel architectures.
Gerhard Niederbrucker (University of Vienna), Wilfried Gansterer (University of Vienna)
Distributed aggregation methods, such as consensus or gossip-based approaches, have been studied intensely in the last decade and many fundamental contributions have been made. These concepts originally target distributed systems, such as sensor networks or P2P systems, and have thus have so far not been considered in high performance computing. Moreover, to the best of our knowledge, some aspects related to realistic distributed computation and the recovery from silent failures have not been addressed in detail so far.
We discuss a general approach for provably reliable distributed aggregation under more realistic assumptions on the computing environment. By taking theoretical as well as practical points of view into account, we point out several issues concerning the practical applicability of the vast amount of existing methods and their analyses. We outline a novel convergence theory for a large class of distributed aggregation algorithms, which is more general than existing work and relies only on purely local assumptions. Based on this more general convergence theory, provably reliable distributed aggregation algorithms can be derived which successfully handle some of the challenges arising in practical computations on realistic systems.
These reliable distributed aggregation methods may also be attractive building blocks for improving resilience at the algorithmic level in tightly coupled extreme-scale parallel systems.
Marc Casas (Polytechnic University of Catalonia), Miquel Moretó ( Polytechnic University of Catalonia), Greg Bronevetsky (Lawrence Livermore National Laboratory), Jesús Labarta (B Polytechnic University of Catalonia), Eduard Ayguadé (Polytechnic University of Catalonia), Mateo Valero (Polytechnic Univers
Since the number of hardware components is expected to grow by one or two orders of magnitude and the circuits' features will also decrease, reliability is expected to be a critical challenge for exascale computing. Specifically, exascale machines are expected to suffer hard faults, i. e., crashes, soft faults, i. e. silent data corruptions, plus performance slowdowns due to unexpected behavior of some hardware components. Several techniques that combine system software, hardware support or algorithmic based fault tolerant solutions have been proposed over the last years. In this talk, we survey them and explain their weak and strong points.
George Bosilca (University of Tennessee), Aurelien Bouteiller (University of Tennessee), Thomas Herault (University of Paris-Sud)
While the need for resilience in applications capable of taking advantage of future computing platforms become evident, the methods toward a comprehensive resilient solution are widely divergent. From totally transparent approaches to alterations of the underlying mathematical algorithm to expose resilient capabilities, all fault management approaches have their applicability domain. Holistic fault tolerance solutions will not come from a unique solution but instead from a mix of different approaches, adapted to the different computational stages. This talk will introduce mixed approaches based on checkpoint/restart and algorithm-based fault tolerance allowing for more flexibility and smaller overheads.
Luc Giraud (INRIA), Emmanuel Agullo (INRIA), Luc Giraud (INRIA), Abdou Guermouche (LaBRI), Jean Roman (INRIA), Pablo Salas (Université de Sherbrooke), Mawussi Zounon (INRIA)
The advent of extreme scale machines will require the use of parallel resources at an unprecedented scale, probably leading to a high rate of hardware faults. Handling fully these faults at the computer system level may have a prohibitive cost. High performance computing applications that aim at exploiting all these resources will thus need to be resilient, i.e., be able to compute a correct solution in presence of core crashes. In this work, we investigate possible remedies in the framework of numerical linear algebra problems such as the solution of linear systems or eigen-problems that are the inner most numerical kernels in many scientific and engineering applications and also ones of the most time consuming parts. More precisely, we present recovery techniques followed by restarting strategies. In the framework of Krylov subspace linear solvers the lost entries of the iterate are interpolated using the available entries on the still alive cores to define a new initial guess before restarting the Krylov method. In particular, we consider two interpolation policies that preserve key numerical properties of well-known linear solvers, namely the monotony decrease of the A-norm of the error of the conjugate gradient or the residual norm decrease of GMRES. We extend these interpolation ideas in the context of some state of the art eigensolvers where these recovery approaches are applied to reconstruct a meaningful search space for restarting. We assess the impact of the recovery method, the fault rate and the number of processors on the robustness of the resulting numerical linear solvers.
Weichung Wang (National Taiwan University), Wen-Wei Lin (National Chiao Tung University), Tsung-Ming Huang (National Taiwan Normal University), Han-En Hsieh (National Taiwan University)
Three dimensional photonic crystals can be modeled by the Maxwell equations as generalized eigenvalue problems. Simulations based on the numerical solutions of the eigenvalue problems are used to reveal physical properties and to boost innovative applications of photonic crystals. However, to solve these eigenvalue problems is a computational challenge. We address how these large-scale eigenvalue problems can be solved efficiently. The tools include an explicit eigendecomposition of the degenerate discrete double-curl matrix, null space free methods, preconditioning schemes, mixed precision eigenvalue solvers, and parallel computers with accelerators such as GPU. Numerical results are promising with a great potential on band-gap engineering applications.
Jose E. Roman (Polytechnic University of Valencia), Carmen Campos
Consider the nonlinear eigenvalue problem  , where
, where  is a matrix function analytic in a given region
is a matrix function analytic in a given region 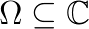 . We are interested in computing a few eigenvalues
. We are interested in computing a few eigenvalues 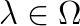 and their corresponding eigenvectors
and their corresponding eigenvectors  of large-scale problems by means of iterative methods.
of large-scale problems by means of iterative methods.
Write the nonlinear operator as 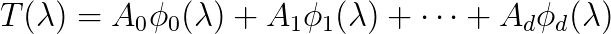 , where
, where 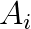 are square matrices (typically sparse) and
are square matrices (typically sparse) and 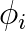 are scalar functions analytic in
are scalar functions analytic in 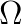 . We will consider the general case of arbitrary nonlinear functions
. We will consider the general case of arbitrary nonlinear functions 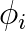 , and also the particular case where
, and also the particular case where 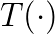 is a matrix polynomial of degree
is a matrix polynomial of degree 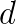 and hence the
and hence the 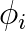 represent the polynomial basis, either monomial or non-monomial.
represent the polynomial basis, either monomial or non-monomial.
When computing more than one eigenpair, it is important to represent the computed solutions by means of invariant pairs 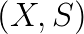 , which generalize invariant subspaces to the nonlinear case. An invariant pair satisfies
, which generalize invariant subspaces to the nonlinear case. An invariant pair satisfies 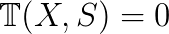 with
with  where here
where here 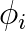 are the corresponding matrix functions. An eigenvalue of matrix
are the corresponding matrix functions. An eigenvalue of matrix 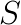 is an eigenvalue of the nonlinear eigenproblem.
is an eigenvalue of the nonlinear eigenproblem.
A computed invariant pair may have considerable numerical error since computational methods for nonlinear eigenproblems, e.g., via linearization, are not always backward stable. Therefore, postprocessing with an iterative refinement strategy is crucial for making the overall solution process robust. Iterative refinement may be based on the block Newton method for nonlinear eigenvalue problems proposed by D. Kressner [Numer. Math. 114 (2009), pp. 355–372]. This process solves the nonlinear matrix equations represented by 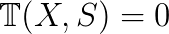 , together with a normalization condition. Furthermore, a specialized version specific for matrix polynomials has been developed by Betcke and Kressner [Linear Algebra Appl. 435 (2011), pp. 514–536].
, together with a normalization condition. Furthermore, a specialized version specific for matrix polynomials has been developed by Betcke and Kressner [Linear Algebra Appl. 435 (2011), pp. 514–536].
The algorithm involves the solution of a correction equation similar to that in the Jacobi-Davidson method, together with operations with the coefficient matrices 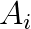 and various vectors. We investigate how to implement it efficiently in parallel, and in the polynomial case how to exploit the structure of the initial solution computed by a Krylov method with linearization. We present results for an implementation within the SLEPc library.
and various vectors. We investigate how to implement it efficiently in parallel, and in the polynomial case how to exploit the structure of the initial solution computed by a Krylov method with linearization. We present results for an implementation within the SLEPc library.
Michael Moldaschl (University of Vienna), Wilfried Gansterer (University of Vienna)
We discuss some general and some application-specific modifications and improvements of distributed orthogonal iteration-based eigensolvers. First, we show how to generically reduce the communication cost by exploiting replicated intermediate results. Thus, we can replace distributed with local operations.
Second, we concentrate on the special case of computing eigenvalue 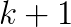 when the
when the 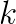 extreme eigenvalues of a given matrix are known. We introduce and compare different methods for fast approximation of this eigenvalue. The core of our approach is a modification of the orthogonal iteration method which may potentially cause some loss of accuracy. We theoretically analyze the convergence behaviour of the modified orthogonal iteration and show how to avoid this loss of accuracy. Furthermore, we show that although this modification is only insignificantly faster in sequential execution, for certain cases it has important advantages in parallel settings. In particular, if the given matrix is the adjacency matrix of the underlying parallel or distributed system, strong reductions of communication cost compared to previously existing distributed eigensolvers are possible. For example, on a hypercube topology, the reduction in the number of aggregation steps across the entire system can be as large as a factor of 15.
extreme eigenvalues of a given matrix are known. We introduce and compare different methods for fast approximation of this eigenvalue. The core of our approach is a modification of the orthogonal iteration method which may potentially cause some loss of accuracy. We theoretically analyze the convergence behaviour of the modified orthogonal iteration and show how to avoid this loss of accuracy. Furthermore, we show that although this modification is only insignificantly faster in sequential execution, for certain cases it has important advantages in parallel settings. In particular, if the given matrix is the adjacency matrix of the underlying parallel or distributed system, strong reductions of communication cost compared to previously existing distributed eigensolvers are possible. For example, on a hypercube topology, the reduction in the number of aggregation steps across the entire system can be as large as a factor of 15.
An important application of our new method arises in Chebyshev acceleration of distributed fixed-point iterations (for example, of average consensus or gossip-based algorithms), where the largest eigenvalue and corresponding eigenvector of the defining matrix is known and the second largest eigenvalue is required for achieving optimal convergence rate. We apply our method in this context and also illustrate the already known performance improvements of Chebyshev acceleration for average consensus, especially for loosely connected parallel or distributed systems.
Yasuyuki Maeda (University of Tsukuba), Tetsuya Sakurai (University of Tsukuba)
In this talk, we present the parallelization approach for the contour integral spectral slicing solver (CISS) in SLEPc. The software library SLEPc for solving large, sparse, eigenvalue problems on parallel environments provides various eigensolvers and singular value decomposition algorithms. SLEPc can be used for solving various eigenvalue problems that include linear, polynomial and nonlinear eigenvalue problems. CISS is one of the eigensolvers in SLEPc that is based on the Sakurai-Sugiura method. The method calculates eigenvalues in a given domain and associated eigenvectors. There are several types of parallelism in the Sakurai-Sugiura method. In this talk, we show parallelization approach to manage these different types of parallelism used in CISS. We create multiple MPI sub-communicators and redundant matrices that are functions in SLEPc. The Sakurai-Sugiura method can also be used for nonlinear eigenvalue problems. SLEPc provides the framework for nonlinear eigenvalue problems. We also describe the implementation of CISS for nonlinear eigenvalue problems on the framework. We evaluate the efficiency of our approach by several numerical examples.
Hiroki Tanaka (Kyoto University), Hiroyuki Ishigami (Kyoto University), Kinji Kimura (Kyoto University), Yoshimasa Nakamura (Kyoto University)
Singular value decomposition facilitates to generate orthonormal basis of the row and null spaces. Singular vectors corresponding to non-zero and zero singular values form an orthonormal basis of the row space and the null space, respectively. If singular values computed do not have relative accuracy, we cannot distinguish easily whether singular values are zero or not. Thus, algorithms which can compute “relatively accurate” singular values and singular vectors with high accuracy are required. In order for us to compute orthonormal basis of the row and null spaces, the numerical algorithm must possess the following two properties. First, the algorithm must compute singular vectors with high accuracy. For this purpose, it is desirable that the algorithm is constituted by a sequence of orthogonal transformations. “Divide and conquer” algorithm (D&C algorithm) and Inverse iteration algorithm (II algorithm) sometimes fail to compute singular vectors. Hence, D&C algorithm and II algorithm are not suitable for the purpose. Secondly, the algorithm must be able to compute “relatively accurate” singular values.
The modified QR algorithm proposed by Demmel and Kahan, and the orthogonal qd-algorithm with shift (oqds algorithm) proposed by von Matt is performed by using sequences of orthogonal transformations. It is to be noted that there is no guarantee that the QR algorithm can compute tiny singular values accurately. On the other hand, the oqds algorithm is guaranteed to compute “relatively accurate” singular values theoretically. However, effective implementation of the oqds algorithm to achieve such performance are not known. Thus, in this talk, we propose two techniques for improving the performance of the oqds algorithm.
First, we improve to generate orthogonal transformations. The oqds algorithm employs the Givens rotation and the generalized Givens rotation. The Givens rotation is actualized by the BLAS1 subroutine "drotg", and the generalized Givens rotation by the original subroutine "drotg3". Instead of using "drotg", we can use the "dlartg" subroutine in LAPACK to actualize the Givens rotation. This subroutine is slower but it is more accurate than "drotg". Moreover, the generalized Givens rotation can be redefined by the product of the Givens rotation and an orthogonal transformation. We can apply "dlartg" to the generalized Givens rotation.
Secondly, we consider an improvement of the convergence speed of the oqds algorithm. We incorporate a new shift of origin into the oqd algorithm in order to accelerate its convergence. It is known that the convergence of the oqds algorithm is accelerated more effectively when the shift value is closer to the smallest singular value of the matrix on each iteration. Acceleration of convergence reduces the number of iterations. The smaller number of iterations provides singular value decomposition with high accuracy since accumulation of rounding errors can be suppressed. In the conventional method, Laguerre's and Newton's methods are used to compute the shift value. However, the shift value computed does not sufficiently accelerate the convergence. Thus, we propose a new shift strategy for the oqds algorithm. The new shift strategy compute a bound of the smallest singular value by using binary search. The shift values computed by the proposed shift strategy are much closer to the smallest singular value than that computed by the conventional shift strategy.
The results of numerical experiments indicate that the improved oqds algorithm performs singular value decomposition with higher accuracy than that of the modified QR algorithm. Both the more accurate Givens rotation and the new shift strategy contribute to compute “relatively accurate” singular values and singular vectors with high accuracy.
The improved oqds algorithm can be parallelized using the same technique as that used by the modified QR algorithm implemented in ScaLAPACK.
Vedran Novakovic (University of Zagreb)
We present a hierarchically blocked one-sided Jacobi algorithm for the singular value decomposition (SVD), targeting both a single and the multiple graphics processing units (GPUs). The blocking structure reflects the levels of GPU's memory hierarchy. The algorithm is faster than MAGMA's DGESVD, while retaining the high relative accuracy. To this end, we developed a family of parallel pivot strategies on GPU's shared address space, but applicable also to inter-GPU communication. Unlike common hybrid approaches, our algorithm in a single GPU setting needs a CPU for the controlling purposes only. When required by the problem size, the algorithm, in principle, scales to an arbitrary number of GPU nodes. The scalability is demonstrated by more than twofold speedup for sufficiently large matrices on a Tesla S2050 system with four GPUs vs. a single Fermi card.
Yuki Fujii (Kyoto University), Hiroyuki Ishigami (Kyoto University), Kinji Kimura (Kyoto University), Yoshimasa Nakamura (Kyoto University)
In this talk, we implement the bisection and inverse iteration (BI) algorithm for symmetric band matrices to singular value decomposition (SVD) for large-scale sparse matrices by using a Krylov subspace method.
We consider SVD of 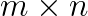 (
( ) matrices. In problems concerning scientific applications such as data search and rank-
) matrices. In problems concerning scientific applications such as data search and rank-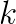 (
( ) approximation,
) approximation, 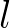 (
( ) singular pairs, i.e. singular values
) singular pairs, i.e. singular values 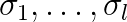 (
(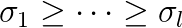 ) and the corresponding singular vectors, are often required. For a large-scale sparse matrix, it is difficult to perform SVD directly with respect to execution time. In this case, the target matrix is transformed into a small matrix whose singular values are approximated well to those of the original matrix as the preprocessing is performed by using Krylov subspace methods.
) and the corresponding singular vectors, are often required. For a large-scale sparse matrix, it is difficult to perform SVD directly with respect to execution time. In this case, the target matrix is transformed into a small matrix whose singular values are approximated well to those of the original matrix as the preprocessing is performed by using Krylov subspace methods.
The Golub-Kahan-Lanczos (GKL) algorithm is a preprocessing algorithm based on the Krylov subspace, and generates an approximate bidiagonal matrix from the original matrix. A singular value problem for the 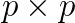 bidiagonal matrix (
bidiagonal matrix (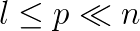 ) is replaced with an eigenproblem for a symmetric tridiagonal matrix in terms of a
) is replaced with an eigenproblem for a symmetric tridiagonal matrix in terms of a  extended matrix. From the
extended matrix. From the  extended matrix,
extended matrix, 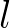 (
( ) singular pairs of the original matrix are obtained. We see that the eigenpair of the extended matrix corresponding to the
) singular pairs of the original matrix are obtained. We see that the eigenpair of the extended matrix corresponding to the 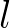 -th singular pair of the original matrix can be also used for stopping this algorithm, where the number of such an eigenpair is just one. For this purpose, it is suitable to employ the BI algorithm.
-th singular pair of the original matrix can be also used for stopping this algorithm, where the number of such an eigenpair is just one. For this purpose, it is suitable to employ the BI algorithm.
The GKL algorithm usually loses the orthogonality of the Krylov subspace owing to computational error. To improve the orthogonality, we need to incorporate reorthogonalization into the GKL algorithm. Such an algorithm is referred to as the reorthogonalized GKL (RGKL) algorithm. Moreover, the block GKL (BGKL) algorithm is a variant of the GKL algorithm, and the corresponding Krylov subspace is generated by using matrix-matrix multiplications. In general, we need to parallelize these algorithms in terms of the operations at each iteration. It is difficult to achieve high-performance parallel processing with the GKL and RGKL algorithm because it is mainly composed of matrix-vector multiplications. Hence, the BGKL algorithm is expected to achieve higher performance in parallel processing than those of the GKL and RGKL algorithm.
Along with the RGKL algorithm, the Reorthogonalized BGKL (RBGKL) algorithm improves the orthogonality of the Krylov subspace from that of the BGKL algorithm. The RBGKL algorithm generates a  approximate block bidiagonal matrix (
approximate block bidiagonal matrix ( ). As with the GKL algorithm, the
). As with the GKL algorithm, the  -th singular pair of the approximate block bidiagonal matrix can also be used for stopping this algorithm. The subject of this talk is to propose efficient computation of the
-th singular pair of the approximate block bidiagonal matrix can also be used for stopping this algorithm. The subject of this talk is to propose efficient computation of the  -th singular pair. Conventionally, we perform this computation by transforming the approximate block bidiaognal matrix into a
-th singular pair. Conventionally, we perform this computation by transforming the approximate block bidiaognal matrix into a 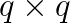 bidiagonal matrix by the Murata method, and computing the
bidiagonal matrix by the Murata method, and computing the  -th singular pair with the BI algorithm for the
-th singular pair with the BI algorithm for the 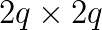 extended matrix. In our approach, we compute the
extended matrix. In our approach, we compute the 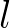 -th singular pair directly for block bidiagonal matrix by using the BI algorithm for a symmetric band matrix in terms of the
-th singular pair directly for block bidiagonal matrix by using the BI algorithm for a symmetric band matrix in terms of the 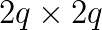 extended matrix.
extended matrix.
To evaluate the proposed implementation, numerical experiments are executed on shared-memory parallel processors. The results show the following properties. In the RBGKL algorithm, the proposed implementation is more suitable for computing the  -th singular pair than the conventional implementation. Then, in many cases, the RBGKL algorithm with the proposed implementation is faster than the RGKL algorithm with the BI algorithm for computing the
-th singular pair than the conventional implementation. Then, in many cases, the RBGKL algorithm with the proposed implementation is faster than the RGKL algorithm with the BI algorithm for computing the 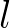 -th singular pair.
-th singular pair.
A. Cristiano I. Malossi (IBM Research - Zurich), Yves Ineichen (IBM Research - Zurich), Costas Bekas (IBM Research - Zurich), Alessandro Curioni (IBM Research - Zurich), Enrique S. Quintana-Ortí (Universidad Jaime I)
While Moore's law is expected to remain valid for approximately one more decade, the end of Dennard scaling (i.e., the ability to shrink the feature size of integrated circuit technology while maintaining a constant power density), which partly motivated the transition to multicore architectures around 2004, is now pushing processor design towards “dark silicon” and, in consequence, heterogeneous systems. The scientific community, as responsible for a large fraction of the energy consumed in today's large-scale computing facilities, is not immune to these trends, and a number of research projects now place energy in par with performance among their goals, in a holistic effort for higher energy efficiency all the way from the hardware to the application software.
Along this line, optimizing the 7/13 “dwarfs”, introduced by UC Berkeley in 2006, represents a challenge with a potential tremendous impact on a vast number of scientific/engineering applications and libraries, which are indeed composed of these computational blocks. However, without a careful modeling and a subsequent understanding of the phenomena, the optimization process of these kernels is doomed to fail.
In this talk, we will analyze the interactions occurring in the performance-power-energy triangle for the sparse matrix-vector product (SpMV), a challenging kernel due to its indirect and irregular memory access pattern. SpMV constitutes the key ingredient of the sparse linear algebra dwarf, as well as for many iterative methods for the solution of linear systems arising in, e.g., boundary value problems, eigenvalue problems, finite element methods, economic modeling, web search, and information retrieval, among others.
In the first part of our analysis, we will identify a set of few critical parameters that drive the performance and instantaneous power consumption of a baseline implementation of the SpMV. We will show the link between these parameters and the algorithmic and architecture features, and on top of them we will build a general classification of sparse matrices, which represents a tool to obtain an instantaneous qualitative indication of the performance-power-energy features of SpMV (i.e., a characterizations along these three magnitudes), based only on a few statistical information about the sparse matrix structure, and independent from the original problem.
In a second step, we will use a small synthetic sparse benchmark collection (the training set) to build a general model which is able to provide accurate quantitative estimations of performance-power-energy for any matrix. To prove the robustness of our methodology, we will test the model against the entire University of Florida Matrix Collection, run on two different high-end multithreaded architectures, representative of state-of-the-art multicore technology.
The model and classification presented here can impact large clusters and cloud systems, where the prediction of performance and energy consumption yields important benefits in terms of, e.g., optimal jobs scheduling and costs prediction, among others.
George Delic (HiPERiSM Consulting, LLC)
This study reports on major performance enhancements for the community multi-scale air quality model (CMAQ) chemistry-transport model (CCTM) that add new levels of parallelism and replace the legacy algorithm in the Gear sparse matrix gas-phase chemistry solver. The role of air quality modeling is to study and predict the chemical interaction, atmospheric transport, and deposition of airborne pollutants on metropolitan, regional, continental and hemispheric scales. CMAQ is a major air quality model used in such studies and was developed by the U.S. Environmental Protection Agency (EPA). It has a world-wide user base of over 2,900 recorded downloads. By applying operator splitting, the CCTM implements multiple science modules that describe various physical processes such as advection, diffusion, photolysis, aqueous chemistry and cloud dynamics, gas-phase chemistry, etc. The gas phase chemistry solver in the CCTM is one of the most computationally intensive modules. It allows a choice of various gas-phase solvers that implement different algorithms for integration of a stiff system of ordinary differential equations (ODE), with sparse Jacobians, to describe production and loss of chemical species in reaction mechanisms. When the Gear algorithm is used for the system of ODEs it accounts for over 50% of the wall clock time of a simulation. To improve performance the new version makes two important changes in the standard EPA CMAQ distribution. The first change replaces the sparse matrix solver used for chemical species concentrations. The second modification integrates the new solver into the transit over grid cells so that separate blocks of cells are distributed to different threads. These modifications were successfully applied to CMAQ with the Rosenbrock solver [1] where the same legacy sparse Gaussian linear solver was replaced. For the Gear ODE algorithm this report describes how the sparse solver (FSparse) replaces the legacy JSparse solver method based on the work of Jacobson and Turco [2]. The FSparse solver is a Fortran implementation of Gaussian elimination procedures from the CSparse library of Davis [3]. The parallel processing limitations of the compressed column sparse storage scheme are overcome by transformations to the compressed row storage scheme after the decomposition phase, and before the solve phase. As a result, the revised Gear solver adds both instruction level parallelism and thread level parallelism to the existing distributed memory (message passing) level in the standard EPA release. Observed numerical differences between the two methods are related to the numerical precision achieved and this is discussed in detail. For a 24-hour simulation on a continental U.S.A. grid of 2.3 million cells, results show that with 8 threads the FSparse version of CMAQ is 1.8 times faster than the standard EPA release of CMAQ with the Gear ODE solver (and is also more accurate). This speedup represents 90% of the theoretical maximum of 2.
[1] G. Delic, 12th Annual CMAS conference, October 28-30, 2013. http://www.cmascenter.org/conference/2013/agenda.cfm. [2] M. Jacobson and R.P. Turco (1994), Atmos. Environ. 28, 273-284 [3] T.A. Davis, Direct Methods for Sparse Linear Systems, SIAM, Philadelphia, 2006.
Dan Gordon (University of Haifa), Rachel Gordon (Technion – Israel Institute of Technology), Eli Turkel (Tel Aviv University)
We consider the Helmholtz equation in 3D: 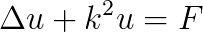 , where
, where  is the displacement at
is the displacement at  ,
, 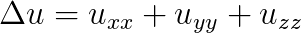 and
and 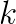 is the wave number. This equation has applications in many fields, such as acoustics and electromagnetism. In geophysics, methods of full wave inversion reconstruct the structure of some volume of the earth from data received by many sensors recording the reflection of sound waves. The frequency domain approach to this reconstruction requires the repeated solution of the Helmholtz equation, in which the RHS function
is the wave number. This equation has applications in many fields, such as acoustics and electromagnetism. In geophysics, methods of full wave inversion reconstruct the structure of some volume of the earth from data received by many sensors recording the reflection of sound waves. The frequency domain approach to this reconstruction requires the repeated solution of the Helmholtz equation, in which the RHS function 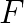 represents an impact source, so it has a small finite support.
represents an impact source, so it has a small finite support.
Due to dispersion errors (also known as the pollution effect), it is well known that problems with wave propagation are solved more efficiently by using high order accurate methods. In addition to high order accuracy, it is also useful to consider only compact stencils ( in 3D). This has several advantages. Foremost, is that no non-physical boundary conditions need be considered. In addition this reduces the bandwidth of the matrix to be inverted. Another practical advantage is that huge 3D domains require parallel solvers, and compact schemes lend themselves more easily to parallel domain decomposition techniques, such as the CARP-CG algorithm [2] used in this work.
in 3D). This has several advantages. Foremost, is that no non-physical boundary conditions need be considered. In addition this reduces the bandwidth of the matrix to be inverted. Another practical advantage is that huge 3D domains require parallel solvers, and compact schemes lend themselves more easily to parallel domain decomposition techniques, such as the CARP-CG algorithm [2] used in this work.
The main difficulty in applying a compact high order finite difference scheme to solve the Helmholtz equation on a geophysical problem is that large geophysical domains consist of different types of materials with different acoustic properties, i.e., the wave number 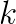 varies within the domain. In this work we use the compact 6th order scheme of [4], which was developed for variable
varies within the domain. In this work we use the compact 6th order scheme of [4], which was developed for variable 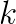 and shown to be far superior to lower order schemes.
and shown to be far superior to lower order schemes.
However, high order finite difference schemes are not enough for correctly simulating the wave equation. The numerical solution is carried out in a finite domain, so in order to simulate an infinite domain, we need to impose so-called absorbing boundary conditions (ABCs) that will inhibit reflections from the boundaries. One of the first ABCs was formulated by Engquist and Majda. An equivalent BC was later formulated by Higdon [3]. For spherical domains, a series of absorbing boundary conditions was developed in [1]. We have developed several compact high order schemes based on these ABCs, including a novel approach for improved accuracy at the corners.
In order to evaluate the various ABCs, we ran experiments on a domain with a constant 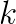 and a known analytic solution. The source was simulated by a function of the type
and a known analytic solution. The source was simulated by a function of the type 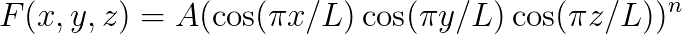 for
for 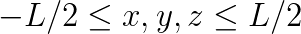 and zero elsewhere.
and zero elsewhere.  is the amplitude,
is the amplitude,  , and
, and  determines the size of the support. Experiments were ran with various frequencies.
determines the size of the support. Experiments were ran with various frequencies.
It is well known that for constant 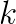 , the analytic solution is obtained by a convolution of
, the analytic solution is obtained by a convolution of 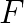 and
and 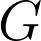 , where
, where 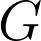 is the Green's function for 3D. The convolution integral was calculated numerically and compared with the solutions obtained by various ABCs.
is the Green's function for 3D. The convolution integral was calculated numerically and compared with the solutions obtained by various ABCs.
In order to determine the quality of the ABCs in absolute terms, the ABC results were compared with the solution obtained when Dirichlet boundary conditions were imposed on the exterior boundaries. The values on the boundaries were determined by the numerical convolution of 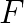 and
and 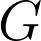 . Obviously, no ABC can do better than such a Dirichlet BC. We conclude with a geophysical application.
. Obviously, no ABC can do better than such a Dirichlet BC. We conclude with a geophysical application.
References
[1] Bayliss, Gunzburger // Turkel. SIAM J. Appl. Math., 1982.
[2] Gordon // Gordon. Paral. Comput., 2010.
[3] Higdon. Math. of Comput., 1987.
[4] Turkel, Gordon, Gordon // Tsynkov. J. Comput. Physics, 2013.
Francois Pacull (Claude Bernard University Lyon 1), Damien Tromeur-Dervout, Stephane Aubert
If parallel algebraic multigrid (AMG) methods are widely used for large sparse linear systems, they are not always the method of choice in the case of strongly non-symmetric matrices arising from systems of partial differential equations (PDE), with tightly coupled scalar unknowns. For example, convection-dominated compressible flows discretized with a high-order central scheme usually yield difficult cases for AMG, in part because of the negligible magnitude of diagonal blocks compared to extra-diagonal ones. Also, they may suffer from the strong anisotropy of flow and mesh.
Here is a brief description of the algorithm of interest: we use the GMRES Krylov subspace iterative solver, preconditioned by AMG. However, the operator for the preconditioning system is not the targeted matrix generated with a high-order scheme, but one discretized with a low-order scheme. In order to apply the preconditioner at each step of the outer GMRES loop, a simple aggregation-based AMG is used. A reduced primary matrix, which coefficients depends on the Frobenius norm of the matrix blocks, is constructed in the coarsening setup phase. The same interpolation strategy is used to interpolate each field. For the smoother, the point-block ILU(0) factorization combined with a line ordering is used locally within some Restricted Additive Schwarz (RAS) preconditioned Richardson iterations. The present line reordering technique consists of several steps: build a weighted quotient graph, each vertex corresponding to a diagonal block, then create sequences of strongly coupled vertices, and finally assemble the sequences in order to form a global permutation. This ordering is found to greatly improve the decomposition quality.
A parallel multilevel graph partitioning algorithm is used first along with a weighted graph, in order to distribute the matrix so as to minimize the coupling between the sub-domains and the amount of communication. Restrictions and prolongations steps can be performed in parallel without any communication. However, the smoothing steps and the coarse solver involve some significant communication. The GMRES method is also set as the coarse grid solver along with a RAS/ILU(0) preconditioner. Although the fine low-order matrix is significantly sparser that the higher-order one, the coarse-grid low-order matrix is quite denser that the fine one.
In order to test the robustness of the proposed method, the cases used in the following originate from compressible aerodynamics, more precisely from discrete direct numerical sensitivity analysis, where accurate flow derivatives are sought. However, the presented method apply to any system of coupled system of PDEs for which point-block algorithms apply. Indeed, the approach is purely algebraic, so that it automatically adjusts itself to any complex domains, discontinuous coefficients and anisotropies. The only requirement is that a linear system discretized with a low-order scheme, e.g. first-order upwind, must be generated alongside the targeted higher-order one. This does not represent a difficulty if the Jacobian matrix is generated by automatic differentiation.
Tom Goffrey (University of Exeter), Jane Pratt (University of Exeter), Maxime Viallet (Max Planck Institute for Astrophysics), Isabelle Baraffe (University of Exeter), Chris Geroux (University of Exeter), Mikhail Popov, Rolf Walder (ENS Lyon), Doris Folini (ETH Zürich)
The evolution of stellar interiors is governed by multi-dimensional non-linear phenomena which occur over a large number of dynamical time scales. To efficiently simulate these hydrodynamic effects a time implicit approach is desirable. Furthermore the physical regime is challenging, due to significant variations throughout a single computational domain. Characteristic parameters such as the Mach number, the density and the pressure scale height can vary by up to ten orders of magnitude over the volume of a star at a single point in its evolution. An outstanding challenge for the field of astrophysical hydrodynamics is to completely resolve flows where Mach numbers typically range from unity to 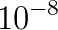 . Without an efficient, scalable and parallel method one cannot expect to simulate stellar processes with the necessary resolution in time or space.
. Without an efficient, scalable and parallel method one cannot expect to simulate stellar processes with the necessary resolution in time or space.
In order to effectively utilise the time implicit approach the resulting matrix system should be efficiently solved, both in terms of memory requirements and the number of iterations needed during the matrix solve. Algebraic preconditioners such as incomplete-LU (ILU) factorisation typically provide scalable, “black-box” tools to improve the solver efficiency. Combining an ILU factorisation with a preliminary block-Jacobi preconditioning step can optimize the preconditioning step and result in fewer iterations. We report on testing of this hybrid preconditioning technique in terms of a reduction in the fill level of the ILU step, and in terms of a simplification of diagonal perturbation methods when compared with pure ILU preconditioning. We then expand this study of the hybrid preconditioning technique by showing preliminary results for stellar processes, including accretion, shear mixing, and turbulent convection.
José I. Aliaga (James I University), Rosa Badía (Barcelona Supercomputing Center), María Barreda (James I University), Matthias Bollhöfer (TU Braunschweig), Enrique S. Quintana-Ortí (James I University)
Over the last decade, we have witnessed a steady increase of thread-level concurrency and hardware parallelism in multicore architectures, leading to processors that nowadays support between dozens and hundreds of threads (e.g., 64 threads in the IBM PowerPC A2 processor and 240 in the Intel Xeon Phi processor). To exploit these architectures, several data-flow programming models have been proposed in the past few years, in with the description of the algorithms are decoupled from its parallel execution, improving portability and coding effort. OmPSs in one of these programming levels.
For the particular domain of dense linear algebra, the application of these models and/or similar approaches has resulted in a collection of high performance libraries (DPLASMA, libflame, MAGMA, PLASMA, etc.). However, the application of data-flow programming paradigms to the parallel solution of sparse systems of linear equations is still unripe, mostly due to sparse linear algebra operations being much more challenging than their dense counterparts.
In this talk, we analyzed how to develop a data-flow parallel version of ILUPACK (incomplete LU decomposition PACKage), available in {http://ilupack.tu-bs.de} for the solution of symmetric positive definite (s.p.d) systems.
Pierre Jolivet (Laboratoire Jacques-Louis Lions), Frederic Nataf (INRIA)
Domain decomposition methods are widely used in applied mathematics and regarded as highly scalable algorithms, alongside multigrid methods. Making those methods scalable to thousands of processors is however not a straightforward task. Projection operators are one of the essential tools for achieving scalability: they are used for building deflation preconditioners. We will present a C++ framework accompanied by theoretical results to show how effective it can be to solve problems with billions of unknowns.
Yushan Wang (University of Paris-Sud), Marc Baboulin (University of Paris-Sud), Karl Rupp, Yann Fraigneau (CNRS), Olivier Le Maître (CNRS)
We describe a hybrid multicore/GPU solver for the incompressible Navier-Stokes equations with constant coefficients, discretized by the finite difference method along with the domain decomposition. By applying the prediction-projection method, the Navier-Stokes equations are transformed into a combination of Helmholtz-like and Poisson equations for which we describe efficient solvers. As an extension of our previous work, we propose a new implementation that takes advantage of GPU accelerators. We present numerical experiments on a current hybrid machine.
Laura Grigori (INRIA), Frederic Nataf (INRIA), Soleiman Yousef (Pierre-and-Marie-Curie University)
In this talk we discuss a robust algebraic preconditioner for solving sparse linear systems of equations involving symmetric and positive definite matrices. The graph of the input matrix is partitioned by using k-way partitioning with vertex separators into N disjoint domains and a separator formed by the vertices connecting the N domains. The obtained permuted matrix has a block arrow structure. The preconditioner relies on the Cholesky factorization of the first N diagonal blocks and on approximating the Schur complement corresponding to the separator block. The approximation of the Schur complement involves the factorization of the last diagonal block and a low rank matrix obtained by solving a generalized eigenvalue problem. The preconditioner can be build and applied in parallel. Numerical results on a set of matrices arising from the discretization by the finite element methodes of linear elasticity models illustrate the robusteness and the efficiency of our preconditioner.
Marc Sergent (INRIA)
The emergence of accelerators as standard computing resources on supercomputers and the subsequent architectural complexity brought back to the forefront the need for high-level programming paradigms. Sequential task-based programming has been shown to efficiently meet this challenge on a multicore node enhanced with accelerators. In this study, we show that this paradigm can also harness clusters of such nodes with extremely limited changes in the user code. To illustrate our discussion, we have extended the StarPU runtime system with an inter-node data management layer and we compare our sequential task-based Cholesky factorization to both the pure Message Passing Interface (MPI)-based ScaLAPACK Cholesky reference implementation and the DPlasma Cholesky code, which implements another (non sequential) task-based programming paradigm.
Benoît Lizé (Airbus Group innovations)
H-Matrix is a hierarchical, data-sparse approximate representation of matrices that allows the fast approximate computation of matrix products, LU and LDLT decompositions, inversion and more. This representation is suitable for the direct solution of large dense linear systems arising from the Boundary Element Method. However, the recursive and irregular nature of these algorithms makes an efficient parallel implementation more challenging, especially when relying on a "Bulk Synchronous Parallel" paradigm. We consider an alternative parallelization for multicore architectures using a task-based approach on top of a runtime system. We show that our method leads to a highly efficient, fully pipelined computation on large real-world industrial test cases in acoustics and electromagnetism.
Alfredo Buttari (University of Toulouse), Emmanuel Agullo (INRIA), Abdou Guermouche (LaBRI), Florent Lopez (University of Toulouse)
To face the advent of multicore processors and the ever increasing complexity of hardware architectures, programming models based on DAG parallelism regained popularity in the high performance, scientific computing community. Modern runtime systems offer a programming interface that complies with this paradigm and powerful engines for scheduling the tasks into which the application is decomposed. These tools have already proved their effectiveness on a number of dense linear algebra applications. This talk evaluates the usability of runtime systems for sparse matrix multifrontal factorizations which constitute irregular workloads, with tasks of different granularities and characteristics and with a variable memory consumption. Experimental results on real-life matrices based on qr_mumps solver and StarPU runtime system show that it is possible to achieve the same efficiency as with an ad hoc scheduler which relies on the knowledge of the algorithm. A detailed analysis shows the performance behavior of the resulting code on homogeneous and heterogeneous architectures.
Eric Darve (Stanford University), Emmanuel Agullo (INRIA), Berenger Bramas (INRIA), Olivier Coulaud (INRIA), Matthias Messner (INRIA), Toru Takahashi(Nagoya University)
Fast Multipole Methods (FMM) are a fundamental operation for the simulation of many physical problems. The high performance design of such methods usually requires to carefully tune the algorithm for both the targeted physics and hardware. In this talk, we present a new approach that achieves high performance across architectures. Our method consists of expressing the FMM algorithm as a task flow and employing a state-of-the-art runtime system, StarPU, to process the tasks on the different computing units. We carefully design the task flow, the mathematical operators, their CPU and GPU implementations as well as scheduling schemes. We assess our method with the StarPU runtime system for executing the resulting task flow on multicore nodes possibly enhanced with GPUs.
Yousef Saad (University of Minnesota), Lin Lin (Lawrence Berkeley National Laboratory), Cao Yang (Lawrence Berkeley National Laboratory), Eric Polizzi (University of Massachusetts Amherst), Eduardo DiNapoli (Forschungszentrum Jülich)
We describe algorithms for two related and important problems: 1) computing the Density Of States (DOS) of a Hamiltonian; 2) Finding the number of its eigenvalues in an interval. These algorithms are based on approximating various filter functions or distributions by polynomial or rational functions. A common ingredient to all methods is to estimate the trace of a matrix via random sampling.
Ahmed H. SAMEH (Purdue University), Alicia Klinvex (Purdue University)
The trace-minimization method – TraceMIN – is a robust parallel eigensolver which is capable of obtaining a few of the smallest eigenpairs of the sparse symmetric eigenvalue problem Ax= λ Bx with a high degree of scalability. Although it has been almost three decades since the algorithm was first published, recent tests have shown that it still compares favorably against newer eigensolvers. Since TraceMIN does not require very accurate solutions to the saddle-point problems that arise in each outer iteration, it can solve problems with which other eigensolvers either struggle or fail. Our most recent implementation of TraceMIN features an additional functionality that some eigensolvers lack: multisectioning (or spectral slicing). This enables finding a large number of eigenpairs belonging to an interior interval of the spectrum. We show that TraceMIN achieves high scalability not only on a single multicore node, but also on clusters consisting of a large number of multicore nodes. Our multisectioning strategy consists of two parts: subdividing the large global interval of interest into many smaller subintervals, and using TraceMIN on each subinterval independently seeking the eigenpairs belonging to the subinterval. Direct sparse solvers such as Pardiso or MUMPS are used to determine the exact number of eigenvalues in each subinterval, as well as for handling the (1,1) block of the saddle-point problems.
Tetsuya Sakurai (University of Tsukuba), Yasunori Futamura (University of Tsukuba), Akira Imakura (University of Tsukuba)
We consider a parallel method for finding interior eigenvalues of a given domain on the complex plane and their corresponding eigenvectors. We have proposed a contour integral-based eigensolver for generalized eigenvalue problems and nonlinear eigenvalue problems. This method is called the SS projection method. In this talk, we present parallel implementation of the SS projection method to utilize hardware potential of large-scale parallel computing environments with many-core architectures. In the SS projection method, a projector is constructed by contour integral of matrix inverse. This operator is regarded as a spectral filter for eigen components. Since the contour integral is approximated by a numerical quadrature, course grained parallelism is obtained for quadrature points. We discuss parallel implementation of the method to achieve good parallel scalability according to the hierarchical structure of the method. By using a filter concept of the SS method, we consider improvement of performance of the method. Software packages z-Pares and CISS that are implementation of the SS method are also introduced. Some numerical experiments are shown to illustrate the performance of our method.
Eric Polizzi (University of Massachusetts), Ping Tak Peter Tang (Intel Corporation), James Kestyn (University of Massachusetts), Brendan Gavin (University of Massachusetts)
The FEAST eigensolver offers a set of important capabilities for achieving high performance, robustness, accuracy, and potential for linear scalability on parallel architectures. The recent detailed numerical analysis of FEAST reported in [SIAM. J. Matrix Anal. & Appl. 35, 354 (2014)], has successfully demonstrated the remarkable convergence properties of the algorithm, and it has also offered new broader perspectives for improvements. In this presentation, new numerical schemes are introduced for the symmetric and non-symmetric FEAST algorithms that can optimize the parallel performances and achieve load balancing for large-scale computing. In particular, we present a new xFEAST scheme that uses a truncated series of generated subspaces. The scheme is not only capable to improve both load balancing and convergence robustness but it also allows, in turn, to reduce considerably the number of linear systems to solve by FEAST contour integrations.
Cosmin Petra (Argonne National Laboratory), Mihai Anitescu (Argonne National Laboratory)
We present a scalable approach that computes in operationally compatible time the optimal energy dispatch under uncertainty for complex energy systems of realistic sizes. Complex energy systems, such as the US power grid, are affected by increased uncertainty of its target power sources, due for example to increasing penetration of wind power coupled with the physical impossibility of very precise wind forecast. The leading optimization-under-uncertainty paradigm for such problems, stochastic programming, requires thousands of simultaneous scenarios, giving problems with billions of variables that need to be solved within an operationally defined time interval.
To address this challenge we have developed PIPS-IPM, a hybrid MPI-SMP parallel solver for stochastic programming problems that uses an interior point method and implements specialized distributed-memory linear algebra. The linear algebra implementation uses a Schur complement technique to obtain a scenario-based parallelization of the computations and, despite the non-trivial decomposition pattern, achieves very high parallel efficiencies on HPC platforms .
To bridge the space between scalability and performance, needed for the real-time solution of stochastic power grid optimization problems, we have recently proposed several algorithmic and implementation advances inside PIPS-IPM. These include a novel incomplete augmented multicore sparse factorization implemented within PARDISO linear solver, coupled with BiCGStab Krylov subspace iterative method to ensure numerical stability and robustness, new multicore- and GPU-based dense matrix kernels, and an efficient implementation of the communication for Cray systems.
We will present large scale simulations of 24-hour horizon dispatch problems with more than 4 billion variables and more than 32 thousands of scenarios on "Titan" Cray XK7 (80% of the machine) of Oak Ridge National Laboratory, "Piz Daint" Cray XC30 (full machine) of Swiss National Computing Centre and "Intrepid" BG/P (80% of the machine) of Argonne National Laboratory. We will discuss several performance metrics of our new developments, such as time-to-solution, peak performance and parallel efficiency, and conclude that solution times compatible with the power grid industry operational practices are possible for this class of optimization problems.
David Horak (Technical University of Ostrava), Vaclav Hapla (Technical University of Ostrava), Lubomir Riha (Technical University of Ostrava), Alexandros Markopoulos (Technical University of Ostrava)
The presentation deals with the ingredients helping us to reach better scalability of the solvers for systems of linear equations and constrained quadratic programming problems. For their solution we develop at IT4Innovations at VSB-TU Ostrava novel software package FLLOP (FETI Light Layer on top of PETSc). It is an extension of PETSc, which is a suite of data structures and routines for the parallel solution of scientific applications modeled by PDE. These solvers can employ direct, iterative or hybrid (combining both previous) methods. Our team has a longterm experience with design and implementation of the scalable domain decomposition methods of FETI type, especially for contact problems, combining iterative a direct solvers. Each method has its pros and cons. We will present bottlenecks of these methods including the strategies for their elimination. A typical example is the coarse problem solution appearing in TFETI method or in deflated conjugate gradient method (DCG). We are able to reach significant improvements using parallel direct solvers in subcommunicators formed by CPUs only or by CPUs accelerated by GPUs/MICs, or using iterative pipelined CG solver applied to the coarse problem matrix better conditioned because of the orthonormalization of the rows of the constrained matrix or the columns of the null space of the stiffness matrix. Numerical experiments illustrate the efficiency of these approaches.
Nerijus Galiauskas (Vilnius University), Julius Žilinskas (Vilnius University)
Finding a step direction in an active-set algorithm for convex quadratic programming problems is the most expensive part of this algorithm. In order to find a step direction we construct and analyze KKT systems. If the KKT system is consistent and has exactly one solution, we solve it by using any solver for systems of linear equations. If the KKT system has more than one solution, we obtain any of them by using a solver for linear least squares problems. If the KKT system is inconsistent, we have to find any eigenvector of the KKT matrix corresponding to the zero eigenvalue. All of these operations (including the analyze of consistency) can be performed by using parallel solvers. Here we present results of numerical experiments related to various strategies how to perform these operations parallelly.
Lukas Pospisil (Technical University of Ostrava), Zdenek Dostal (Technical University of Ostrava)
Numerical solution of many engineering problems, including semicoercive problems of a particle dynamics, leads to the problem of minimizing a convex quadratic function subject to a simple linear inequalities.
This problem is given by
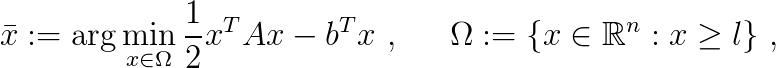 where
where 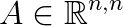 is a symmetric positive semidefinite matrix,
is a symmetric positive semidefinite matrix, 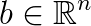 is a right-hand side vector, and
is a right-hand side vector, and 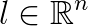 is a vector of bound constraints. To include the possibility that not all the components of
is a vector of bound constraints. To include the possibility that not all the components of 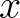 are constrained, we admit
are constrained, we admit 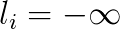 .
In this paper, we propose a modification of recently developed Modified Proportioning with Reduced Gradient Projection (MPRGP) method. This algorithm combines the conjugate gradient steps with the reduced gradient projection steps. Optimality of MPRGP was recently demonstrated on the solution of a class of problems with spectrum of
.
In this paper, we propose a modification of recently developed Modified Proportioning with Reduced Gradient Projection (MPRGP) method. This algorithm combines the conjugate gradient steps with the reduced gradient projection steps. Optimality of MPRGP was recently demonstrated on the solution of a class of problems with spectrum of  in a given positive interval.
Our modification, MPRGP-SPS, converges for any well-posed problem.
in a given positive interval.
Our modification, MPRGP-SPS, converges for any well-posed problem.
The efficiency of our algorithm is illustrated on the solution of granular dynamics problem. Our benchmark consists of moving sphere particles and static box obstacles. In every time-step, we construct the object function from the contacts in the system. Because of the special structure of the matrix  , we are also able to construct the projector onto null space. Then, this projector is used in our algorithm.
, we are also able to construct the projector onto null space. Then, this projector is used in our algorithm.
Michele Martone (Max Planck Institute of Plasma Physics),
Sparse Basic Linear Algebra Subroutines (or `Sparse BLAS') type computations (e.g. triangular solution and multiplication by a vector — respectively SpSV and SpMV) constitute the computational kernel of several scientific and technical computing applications, often being their bottleneck. The memory intensive and irregular features of these computations (foremost, their memory access patterns) make their optimization difficult. An approach that has recently proven to be efficient on shared memory parallel, cache based machines (that is, the `traditional' architectures) is that of a recursive memory layout of the matrix coefficients and coarse grained parallelism in the computations. This approach, that we name `Recursive Sparse Blocks' (RSB) is based on a `cache blocking' like heuristic. In recent work [PARCO_J_14], RSB proved to be competitive with respect to the industry standard Intel MKL CSR implementation and the state-of-the-art CSB prototype, especially when used in SpMV on large symmetric matrices, or with the transposed unsymmetric SpMV operation. Apart from the two operations above, the Sparse BLAS standard specifies also the SpSV operation and provides support for an arbitrary number of right hand sides (`NRHS') and array strides (respectively `INCX' and `INCY') for the two vector operands. An SpMV/SpSV approach that is optimal for the commonest case — one right hand side (NRHS=1) and unitary stride (INCX=INCY=1) — will likely not be optimal for other cases as well, for the memory access pattern will differ substantially. A goal of RSB is to be efficient on the different cases as well, and on the four canonical `BLAS' numerical types.
The present work addresses the problem of tuning our recursive layout for any of the variants of the SpMV and SpSV operations by means of an empirical auto-tuning approach.
That is, given an RSB matrix instance and a SpMV/SpSV operation specification (e.g. NRHS,INCX,INCY), we trade time of search of a `tuned' instance variant for time saved in subsequent, shorter iterations of the same operation. This is possible by re-blocking the matrix differently so it will exhibit a `better' (more efficient) memory access pattern in the given operation.
We present efficient multi-threaded algorithms to support auto-tuning in RSB. On a significant set of real-world matrices, we show that a tangible speedup (over what already exceeds the Intel MKL or the CSB) is still possible. Although results differ widely depending on the matrix structure, type and operation variant, in most of the cases the auto-tuning time can be amortized within a few hundred of iterations.
To confirm the Sparse BLAS oriented spirit of our work, our study extends to all the four the BLAS numerical types, transposition and symmetry and multiple right hand sides variants of the triangular solve and multiply operations.
Since the Sparse BLAS standard interface does not address the case of an `auto-tuning request' by the user, an appropriate extension would be appropriate; we comment this aspect as well.
[PARCO_J_14] http://dx.doi.org/10.1016/j.parco.2014.03.008
Weifeng Liu (University of Copenhagen), Brian Vinter (University of Copenhagen)
Sparse matrix-vector multiplication (SpMV) is perhaps the most widely used non-trivial sparse BLAS routine in computational science and modeling. Compared to CPUs, modern graphics processing units (GPUs) promise much higher peak floating-point performance and memory bandwidth. Thus a lot of research has focused on GPU accelerated SpMV. However, most of them were concentrating on developing new sparse matrix formats (e.g. HYB, Cocktail and BBCOO) constantly challenging well-established scientific software and legacy codes. Further, improving performance of SpMV based on the most widely supported compressed sparse row (CSR) format was largely ignored on GPUs.
Our work described in this paper particularly focuses on accelerating the CSR-format based SpMV on GPUs. Our main contribution is proposing an efficient and general segmented reduction algorithm that directly supports possible empty rows in the input matrix. Note that the empty-row problem actually prevents the classical parallel segmented reduction method from being a general building-block of fast GPU SpMV. Previous work on CSR-format based GPU SpMV either made a strong assumption (i.e. the input matrix is empty-row free) or used pre and post global permutation operations for squeezing the possible empty rows out and inserting them back. Our method, in contrast, deals with the empty rows at runtime and eliminates the costly global permutation operations. Therefore the performance of the CSR-format based SpMV can be significantly improved for general input matrices.
Our algorithm includes 5 steps: (1) The CSR column index array and value array are evenly decomposed to `t' tiles. These tiles are assigned to `b' thread-bunches (i.e. warps or wavefronts). (2) Each GPU thread-bunch executes binary search of `t/b+1' tile boundaries on the CSR row pointer array and obtains corresponding row indices. (3) Each GPU thread-bunch runs `t/b' iterations in a loop to accomplish the following work: (3a) generating localized bit-flag array, (3b) marking tiles to dirty while one or more bit-flag conflicts are detected, (3c) calculating and saving candidate result entries, (3d) executing segmented reduction on them and transmitting the sum of the last segment to next iteration, (3e) storing the segmented sums to known locations in the result vector, and (f) writing the first and the last sum results of all inner iterations to a calibration array of size `2b' in the global memory. (4) The calibration array writes its values to the corresponding entries in the result vector. Then the result vector is numerically correct, except some values generated by these dirty tiles are not in their correct locations. (5) Finally, only for the dirty tiles, our method checks empty rows in the CSR row pointer array and scatter the saved compact results to their correct positions in the result vector. Then the SpMV operation is done.
To evaluate our method, we choose 9 representative unstructured matrices (boyd2, dc2, ASIC_680k, ins2, rajat21, c-73b, transient, wiki-Talk and FullChip) from the University of Florida Sparse Matrix Collection. Compared with state-of-the-art CSR-format based SpMV methods in the nVidia CUSP library (as well as the CUSPARSE library with similar execution pattern and performance) on an nVidia GeForce GTX 680 GPU, our method obtains 5.1x on average and up to 7.9x speedup. Additionally, our method is implemented in OpenCL thus diverse platforms are supported. Compared to our SpMV performance on the nVidia GPU, we achieve 5% on average and up to 83% extra speedup on an AMD Radeon HD 7970 GPU.
Emanuel H. Rubensson (Uppsala University), Elias Rudberg (Uppsala University)
We present a library for efficient block-sparse matrix-matrix multiplication on distributed memory clusters with GPU:s. The library is based on the Chunks and Tasks programming model [Parallel Comput., in press (2013)], allowing it to be implemented without explicitly worrying about communication between the nodes in the distributed memory cluster. On each node, any available GPUs are used for matrix-matrix multiplication tasks. When all GPUs are busy, tasks are also running on the available CPUs, thus making use of the full computing capacity of each node.
Our algorithm is based on a sparse hierarchical data structure [J. Comput. Chem. 28, 2531 ( 2007)] represented by a hierarchy of chunks. The leaves in the hierarchy are block-sparse submatrices. Sparsity may occur at any level in the hierarchy and/or within the submatrix leaves. Both work and data is distributed dynamically over the compute resources, allowing the library to handle unknown and irregular sparsity patterns.
Overlap between computation and communication is achieved for both the data transfer between nodes in the distributed memory cluster and for the data transfer to/from GPUs.
We evaluate the performance of the matrix-matrix multiplication implementation for matrices from linear scaling electronic structure calculations; block-sparse matrices with small block size 16-32, and a priori unknown sparsity patterns. Matrix-matrix multiplication for such matrices is a major computational challenge for large-scale electronic structure calculations.
Pawan Kumar (Fraunhofer ITWM)
In a Schur complement based domain decomposition method, we need to solve for the Schur complement system. The solution for the domain is determined from the solution on the interface, i.e., from the solution of the Schur complement system. For elliptic PDEs under certain conditions, the condition number of the Schur complement system is 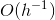 which is already a much better conditioned system than
which is already a much better conditioned system than 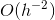 condition number of the global problem. However, the Schur complement matrix itself is not available explicitly, consequently, some of the approaches such as incomplete factorization that are easily applicable when solving the global linear system is not directly applicable when solving the Shur complement system. Nevertheless, countless preconditioners have been proposed for the Schur complement system.
condition number of the global problem. However, the Schur complement matrix itself is not available explicitly, consequently, some of the approaches such as incomplete factorization that are easily applicable when solving the global linear system is not directly applicable when solving the Shur complement system. Nevertheless, countless preconditioners have been proposed for the Schur complement system.
In this talk, we study a parallel deflation based preconditioning for the Schur complement system for problems with highly discontinuous coefficients. We use the existing FGMRES framework to obtain deflation vectors and update the preconditioner during the iterations. The deflation vectors are the approximate Ritz vectors corresponding to real part of eigenvalues close to zero. We show scalability of our approach using global address space programming framework (GPI) provided by GPI library for inter-node as well as inter-socket communication, and C++-11 threading on local cores residing within each sockets. We use the asynchronous and one sided communications provided by GPI to hide the latencies at various phases of the iterative solver. The parallel efficiency and robustness of the proposed preconditioner is validated for convection diffusion problems discretized using finite difference method. We also briefly discuss the parallel partitioning and matrix assembly of the test problem we consider.
Krzysztof Rojek (Częstochowa University of Technology), Lukasz Szustak (Częstochowa University of Technology), Roman Wyrzykowski (Częstochowa University of Technology)
The general purpose programming on graphics devices is currently supported by two main vendors of GPUs. AMD and NVIDIA deliver powerful platforms, which peak performance exceeds a few TFlop/s. The goal of our research is to develop an efficient and portable adaptation of stencil-based 3D MPDATA algorithm to both types of GPUs, including NVIDIA GeForce GTX Titan and AMD FirePro W8000. Differences between these architectures force users to develop distinct approaches and optimizations for each of them, including algorithm configuration, memory management and organization of computation. In this paper, we propose a performance model, which allows for the efficient distribution of computation across GPU resources. Since MPDATA is strongly memory-bounded, the main challenge of providing a high-performance implementation is to reduce GPU global memory transactions. For this purpose, our performance model ensures a comprehensive analysis of transactions based on local memory utilization, sizes of halo areas (ghost zones), data dependencies between and within stencils. The results of analysis performed using the proposed model are number of GPU kernels, distribution of stencils across kernels, as well as sizes of work-groups for each kernel. The best solution selection should be based on maximizing the GPU occupancy, and minimizing resource requirements simultaneously. However, such a solution does not exist, as the optimization criteria are conflicting. So to solve the problem of optimal mapping stencils onto kernels, we base on minimization of GPU memory transactions with constraints taking into account the GPU occupancy. The proposed model is one of the key components for developing an autotuning mechanism dedicated not only to the MPDATA computations, but also to the whole family of stencil algorithms. This mechanism aims at providing the performance portability for OpenCL codes across different GPU architectures.
Jens Saak (Max Planck Institute for Dynamics of Complex Technical Systems), Martin Köhler (Max Planck Institute for Dynamics of Complex Technical Systems)
The Basic Linear Algebra Subprogramms (BLAS) are the core pieces of all scientific computing codes that employ linear algebra operations. Their improvement has been the focus of many researchers and hardware manufacturers since their introduction in late 1980s. Today highly optimized versions for almost any plattform do exist. Still, especially for debugging or profiling purposes switching between the netlib.org reference implementation and optimized versions is a common task that can be rather time consuming when many parts of the project rely on the BLAS.
Reinventing basic ideas of the liftracc project (https://github.com/pc2/liftracc) with an entirely new focus, we present a wrapper library and tools for easy switching and basic profiling of BLAS libraries in the aforementioned code development process. FlexiBLAS allows switching between available BLAS implementations via user hosted configuration files or environment variables at runtime. Thus the need for time consuming recompilations is completely avoided and a smooth workflow is guaranteed. Moreover simple profiling, like counting BLAS calls and timing their execution, comes at basically no user effort and with minimal runtime overhead.
Daniel Ruprecht (Università della Svizzera italiana), Robert Speck (Forschungszentrum Jülich), Rolf Krause (Università della Svizzera italiana)
The “parallel full approximation scheme in space and time”, PFASST for short, has been introduced in 2012 by Emmett and Minion. PFASST is an iterative multilevel strategy for the temporal parallelization of ODEs and discretized PDEs. It is based on “spectral deferred corrections”, an iterative method for solving collocation problems by “sweeps” of a low order time-stepper, e.g. implicit Euler. The combination of an iterative time integration method in each step with an outer iteration passing forward updated initial values can lead to very good parallel efficiency: In benchmarks on 448K cores the space-time parallel combination of PFASST with a parallel multi-grid (PMG) showed significantly better strong scaling than the space-parallel PMG alone.
In order to achieve good parallel efficiency with PFASST, a suitable coarse level representation of the problem has to be derived: Coarse sweeps have to be computationally cheap but must still be accurate enough for the method to quickly converge. For the solution of time-dependent PDEs, several strategies can be used to reduce the accuracy of the spatial representation of the problem on the coarse levels. In particular, when an implicit or semi-implicit method is used for sweeps, it is possible to solve arising (non-)linear only incompletely, e.g. by a fixed small number of multi-grid V-cycles. However, the iterative nature of SDC and PFASST allows to push this approach even further and to also use incomplete solves on the fine level, to reduce overall computation time. This approach leads to so-called “inexact spectral deferred corrections” or ISDC. While ISDC will typically require more sweeps, each sweep becomes significantly cheaper so that in total computation time can be save. Recently, this approach has also been shown to be applicable for PFASST.
The talk will present SDC as a preconditioned Picard iteration and its extension to MLSDC and PFASST. Different coarsening strategies will be discussed, in particular the possibility of “reduced implicit solves”. Several benchmarks showing parallel performance for runs on hundreds of thousands of cores will be presented.
Daniel Hupp (ETH Zurich), Peter Arbenz (ETH Zurich), Dominik Obrist (University of Bern)
Many problems in science and engineering are driven by time-periodic forces. In fluid dynamics, this occurs for example in turbines, or in human blood flow. If the fluid is excited for long enough, it establishes a time-periodic steady state, or at least can be approximated by one. To compute this steady state, classically one starts with some initial guess and lets it evolve through time-stepping until the periodic steady state is reached. We use another approach by solving directly for the steady-state solution, introducing the periodicity as boundary conditions in time. We use a multiharmonic ansatz for the time discretization. This allows to exploit further parallelism, not only in space but also in time. We compare the parallelization capabilities of the classical approach with the time-periodic approach. Furthermore, we compare the performance of both approaches with regard to accuracy and time-to-solution.
Hui Zhang (University of Geneva), Martin J. Gander (University of Geneva), Yao-Lin Jiang (Xinjiang University), Bo Song (Xi'an Jiaotong University)
Time-periodic problems appear typically in special physical situations, for example in eddy current simulations, or when periodic forcing is used, like for periodically forced reactors. The numerical simulation of time- periodic problems is a special area of research, since the time periodicity modifies the problem structure and solution methods significantly. When the scale of the problems increases, it is desirable to use parallel methods to solve such problems, and various kinds of parallel methods have been proposed to solve time-periodic problems in the literature, such as multigrid methods, and waveform relaxation methods, which have proved to be quite effective for time-periodic problems.
All these methods use however spatial parallelism as an essential ingredient. Over the last few years, model order reduction methods have been developed, in order to solve systems of lower dimension instead of the original large-scale systems of differential equations, and in such models often the parallelization in space saturates rapidly. In this work, we are interested in the time direction for parallelization of time-periodic problems.
The parareal algorithm is such a time-parallel method that was proposed by Lions, Maday, and Turinici in the context of virtual control to solve evolution problems in parallel. In this algorithm, initial value problems are solved on subintervals in time, and through an iteration, the initial values on each subinterval are corrected to converge to the correct values of the overall solution. We develop in this work two parareal type algorithms for time-periodic problems: one with a periodic coarse problem, and one with a non-periodic coarse problem. An interesting advantage of the algorithm with the non-periodic coarse problem is that no time periodic problems need to be solved during the iteration, since on the time subdomains, the problems are not time-periodic either. We prove for both linear and nonlinear problems convergence of the new algorithms, with linear bounds on the convergence. It is interesting to note that the parareal algorithms for time-periodic problems do not seem to have a superlinear convergence regime, in contrast to the classical parareal algorithm for initial value problems. We also extend these results to evolution partial differential equations using Fourier techniques. We illustrate our analysis with numerical experiments, both for model problems and the realistic application of a nonlinear cooled reverse-flow reactor system of partial differential equations.
Stephanie Friedhoff (Tufts University), Robert D. Falgout (Lawrence Livermore National Laboratory), Tzanio V. Kolev(Lawrence Livermore National Laboratory), Scott P. MacLachlan (Tufts University), Jacob B. Schroder (Lawrence Livermore National Laboratory)
With current trends in computer architectures leading towards systems with more, but not faster, processors, faster time-to-solution must come from greater parallelism. These trends particularly impact the numerical solution of the linear systems arising from the discretization of partial di fferential equations with evolutionary behavior driving the development of algorithms that allow temporal parallelism. While two-level methodologies, such as parareal, are well-established for parallel-in-time integration, true multilevel approaches remain uncommon. In this talk, we present one such technique, derived based on multigrid reduction principles. The resulting multigrid-reduction-in-time (MGRIT) algorithm is a non-intrusive approach, which only uses an existing time propagator and, thus, easily allows one to exploit substantially more computational resources than standard sequential time stepping. We discuss progress to date in applying MGRIT to parabolic (space-time) problems. In particular, we demonstrate that MGRIT offers excellent strong and weak parallel scaling up to thousands of processors for solving diff usion equations in two and three space dimensions.
Yousef Saad (University of Minnesota)
This talk will be about two different strategies for extracting extreme or interior eigenvalues of large sparse (Hermitian) matrices. The first is based on a polynomial filtering technique. This general approach can be quite efficient in the situation where the matrix-vector product operation is inexpensive and when a large number of eigenvalues is sought, as is the case in electronic structure calculations for example. However, its competitiveness depends critically on a good implementation. The method presented relies on a combination of the Lanczos algorithm with partial reorthogonalization and polynomial filtering based on least-squares polynomials. The second approach we discuss represents ongoing work based on using domain-decomposition type techniques. This approach relies on spectral Schur complements combined with Newton's iteration. This method is particularly appealing for interior eigenvalue problems.
Jonas Thies (German Aerospace Center), Moritz Kreutzer (University of Erlangen-Nuremberg), Martin Galgon (University of Wuppertal), Andreas Pieper (University of Greifswald)
When aiming to compute interior eigenvalues of a large sparse matrix, many iterative techniques (e.g. shift-invert Krylov, Jacobi-Davidson or FEAST) require the solution of linear systems with a `shifted' operator 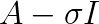 . Even for positive definite matrices
. Even for positive definite matrices 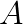 this operator is indefinite for shifts in the interior of the spectrum. We use FEAST as the `outer' eigenvalue iteration, and present a two-level parallel row projection method for the `inner' linear systems. The algorithm and its implementation are describeed, and numerical experiments with large matrices from quantum mechanical applications are shown to demonstrate the performance of the approach.
this operator is indefinite for shifts in the interior of the spectrum. We use FEAST as the `outer' eigenvalue iteration, and present a two-level parallel row projection method for the `inner' linear systems. The algorithm and its implementation are describeed, and numerical experiments with large matrices from quantum mechanical applications are shown to demonstrate the performance of the approach.
Lukas Krämer (University of Wuppertal), Martin Galgon (University of Wuppertal), Bruno Lang (University of Wuppertal)
The FEAST algorithm was introduced by E. Polizzi in 2009 as a method for
the solution of certain eigenvalue problems, in particular 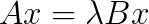 ,
where
,
where 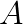 is Hermitian and
is Hermitian and 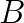 Hermitian positive definite. In this talk, we
present recent work regarding this algorithm.
Hermitian positive definite. In this talk, we
present recent work regarding this algorithm.
First, results concerning the reliability of the method will be shown. This includes the estimation of the number of eigenvalues in an interval, the choice of a basis for the search space and the implementation of additional stopping criteria.
We then present an approach for the solution of the arising linear systems for the special case of dense narrow-banded systems. Further, we identify a method for complex shifted systems that allows solution in real arithmetic.
Finally, we introduce a technique based on a transformation of the integration region that leads to significant improvements with respect to iteration counts (and hence the number of linear systems solves) when seeking extremal eigenvalues.
Matthias Bollhöfer (TU Braunschweig), Andre Bodendiek (TU Braunschweig)
Symmetrically structured problems are a frequently appearing subject, when e.g. solving systems with symmetrically structured matrices or in the symmetrically structured eigenvalue problems. Of particular interest is the case of symmetric and indefinite problems, as modern preconditioned Krylov subspace methods may rely on a symmetric but indefinite preconditioner as well. Moreover, in cases where many systems have to be solved successively, we wish to reuse as much information as possible. Examples, where these problems arise are, e.g., model order reduction problems for symmetrically structured problems based on moment matching like they arise in when being applied to Maxwell's equations. Another example is the computation of interior eigenvalues for symmetric eigenvalue computations, e.g., using the Jacobi-Davidson method. This will present a novel recycling QMR method for symmetrically structured matrices (rSQMR). We will demonstrate its effectiveness in symmetric model order reduction problems and interior eigenvalue computations when using a symmetric but indefinite preconditioner.
Toshiyuki Imamura (RIKEN AICS), Yusuke Hirota (RIKEN), Takeshi Fukaya (RIKEN), Susumu Yamada (JAEA), Masahiko Machida (JAEA)
EigenExa is a high performance and highly scalable dense eigenvalue solver for massively parallel supercomputer systems like K computer. In the present supercomputer system has number of processor units and we must be aware of highly parallelism. Since one of the significant viewpoints for numerical libraries is sequential and parallel performance, we have to adopt adequate algorithms which breaks wall of technologies like a wall of memory bandwidth and network latency. In modern numerical libraries, the multistage reduction scheme is often used to obtain a tri-diagonal matrix when we solve an eigenvalue problem. It extracts good performance improvement since most of the operations in the scheme can be constructed by matrix-matrix product. However, it is pointed out that the cost of backtransformation doubles and the multi-stage is only suitable for computing a part of eigenmodes. To overcome the drawback in the backtransformation and to keep taking advantage of the main idea of the multi-stage reduction algorithm, we investigate a new approach to solve eigenvalues and corresponding eigenvectors. The algorithm is a straightforward solution to avoid the double backtransformation. An outline of the algorithm is as follows; 1) it transforms an input dense matrix to a banded one, 2) and solves the eigen-problem of the derived banded matrix without tri-diagonalization process, 3) then back-transformation for eigenvectors is carried out once. EigenExa employs the divide and conquer method (DC) for a banded matrix discussed in early 1990’s. We implemented the parallel block Householder transformation routine and parallel version of the DC routine of a banded matrix by modifying pdsyevd of ScaLAPACK. The latest version of the EigenExa library performs excellently on several peta-scale computer systems, K-computer, and IBM BlueGene/Q. EigenExa is used in a lot of application code for nano-science, quantum chemistry, and so on. The most outstanding result of EigenExa is that it successively solves a world largest scale dense eigenvalue problem, whose dimension is one-million, within one hour by taking account of the full-node of the K-computer system (82,944 processes, 663,552 cores). The performance reaches approximately 1.8 PFLOPS. This result implies that diagonalization of hundred-thousand dimension matrix is not challenging but feasible on peta-scale computer systems. In the next half decade, exascale computing is one of the biggest issues for the HPC community, indeed, RIKEN has started the development of an exascale computer system as a successor of K-computer. Development of numerical libraries on the exascale system is our biggest challenge. EigenExa will be updated step by step towards the exascale computer system. As it is said that memory bandwidth and network latency are significant in modern parallel computing, to break them will be still significant on exascale computing. In fact, we recognize that ‘communication avoiding’ is one of the biggest issues in order to obtain high performance and high scalability. It does not simply refer to the reduction of the number of communication or message size, but also includes other asynchronous optimization techniques such as ‘communication hiding’ and ‘synchronous avoiding’. Another point towards exascale computing is the adaptation of upcoming hardware architectures as well as programming framework. Since GPU and many-core processors, or their extensions are supposed to be a key technology for next-generation micro-processors, we are going to adopt hierarchical algorithm and parallel implementation in order to map sub-problems onto adequate hardware resources. In the presentation, we would like to introduce the above-mentioned technical issues. Some of details of the latest benchmark results and perspectives of EigenExa towards exascale computing will be shown.
Yusuke Hirota (RIKEN), Toshiyuki Imamura (RIKEN)
In this talk, we describe the solution method for generalized eigenvalue problems (GEP) of matrices 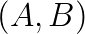 by taking account of manycore processors. Here,
by taking account of manycore processors. Here,  and
and 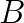 are
are 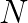 -by-
-by-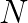 symmetric banded matrices with half bandwidth
symmetric banded matrices with half bandwidth 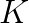 , and
, and 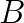 is supposed to be positive-definite. This type of GEPs appears in quantum chemistry typically. In such circumstance, we often see that the matrices are quite narrow that
is supposed to be positive-definite. This type of GEPs appears in quantum chemistry typically. In such circumstance, we often see that the matrices are quite narrow that 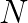 is approximately
is approximately 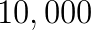 and
and 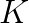 is less than
is less than 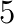 . Thus the acceleration of the solver of the GEPs of such narrow band matrices is important.
. Thus the acceleration of the solver of the GEPs of such narrow band matrices is important.
Computational approaches to solve GEPs for banded matrices (GEPB) is to reduce thin format to narrow by special similarity transformation (e.g. DSBGVD in LAPACK). The half of the operations in this transformation are cache inefficient. In addition, some building blocks of the methods are difficult to be parallelized efficiently. Rough analysis suggests that the conventional approach offers only poor performance on manycore architectures.
We have recently proposed an alternative divide and conquer method for GEPB based on the method for tridiagonal GEPs (Elsner, 1997). The proposed method is summarized by three steps: (1) decomposing the matrices  and
and  to
to 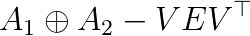 and
and 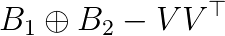 respectively, where
respectively, where 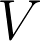 is an
is an  -by-
-by- matrix and
matrix and 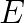 is an
is an 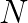 -by-
-by-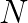 diagonal matrix, (2) solving the sub GEPs of
diagonal matrix, (2) solving the sub GEPs of 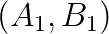 and
and 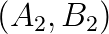 , (3) computing the eigenpairs from the solutions of the sub GEPs, V and E. It is noteworthy that both A and B are expressed with the same matrix V. Alternative decomposition
, (3) computing the eigenpairs from the solutions of the sub GEPs, V and E. It is noteworthy that both A and B are expressed with the same matrix V. Alternative decomposition  and
and  , where
, where  and
and 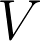 are not identical, results the number of floating point operations (FLOPs) double. The number of FLOPs of the proposed method is
are not identical, results the number of floating point operations (FLOPs) double. The number of FLOPs of the proposed method is  . It is less than the conventional methods when
. It is less than the conventional methods when  is small. The number of FLOPs for matrix multiplications of large matrices in step (3) is the dominant part of the method. Thus, it can be expected that proposed method works faster than conventional methods with only CPU and is accelerated efficiently by using manycore processor.
is small. The number of FLOPs for matrix multiplications of large matrices in step (3) is the dominant part of the method. Thus, it can be expected that proposed method works faster than conventional methods with only CPU and is accelerated efficiently by using manycore processor.
We conduct two preliminary experiments on an environment with an Intel Xeon E5-2660 (2.2 GHz, octa-core, 140.8 GFLOPS) and an Intel Xeon Phi 3120P (57 cores, 1.003 TFLOPS) to evaluate the proposed method and the conventional methods. First, we evaluate the performance of a self-coded implementation of the proposed method and the implementation of the conventional one (DSBGVD, Intel MKL 11.1) using only the CPU. The execution time of computing all eigenpairs of banded matrices ( ,
, 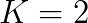 ) of the proposed method is 53.9 seconds which is 18.5 times faster than the conventional one. Secondly, we evaluate parallel version, which is modified to offload large dimensional matrix multiplications to Xeon Phi from the CPU-only version. The execution time of the proposed method is 34.7 seconds and it is 29.3 times faster than the conventional method. The value on a Xeon Phi represents speed-up of 1.55 times in comparison to the CPU-only version. In the experiment, the matrix data for matrix multiplications are transferred between the CPU and the coprocessor redundantly. Thus, the acceleration rate of the proposed method can be better. The results imply that the proposed method is faster than the conventional method on both ordinary CPU and manycore processor. In addition, the proposed method shows the higher acceleration rate on many core processors.
) of the proposed method is 53.9 seconds which is 18.5 times faster than the conventional one. Secondly, we evaluate parallel version, which is modified to offload large dimensional matrix multiplications to Xeon Phi from the CPU-only version. The execution time of the proposed method is 34.7 seconds and it is 29.3 times faster than the conventional method. The value on a Xeon Phi represents speed-up of 1.55 times in comparison to the CPU-only version. In the experiment, the matrix data for matrix multiplications are transferred between the CPU and the coprocessor redundantly. Thus, the acceleration rate of the proposed method can be better. The results imply that the proposed method is faster than the conventional method on both ordinary CPU and manycore processor. In addition, the proposed method shows the higher acceleration rate on many core processors.
Yasunori Futamura (University of Tsukuba), Tetsuya Sakurai (University of Tsukuba)
In this talk, we introduce our parallel software package named z-Pares for solving generalized sparse eigenvalue problems. Z-Pares implements the Sakurai-Sugiura method proposed in 2003 and its variants. This method computes an eigen-subspace using complex moments that are obtained by contour integral. z-Pares can compute eigenvalues located in a specified contour path and corresponding eigenvectors of general non-Hermitian problems. The matrix symmetry and definiteness are appropriately exploited to reduce the computational complexity. z-Pares provides two-level MPI distributed parallelism. The first level is the parallelism for solving independent linear systems with respect to quadrature points and the second level is the parallelism of matrix and vector operations. This feature enables users to utilize a large amount of computational resources. We present performance evaluations z-Pares using large-scale matrices from some practical applications.
Takahiro Yano (University of Tsukuba), Yasunori Futamura (University of Tsukuba), Tetsuya Sakurai (University of Tsukuba)
We consider an implementation of parallel eigensolver for dense generalized eigenvalue problems on distributed GPU systems.
In recent years, a complex moment based method which can solve non-Hermitian generalized eigenvalue problems has been developed. The method constructs a subspace by solving independent linear systems and then desired eigenpairs are extracted from the space. We can obtain a coarse-grained parallelism because of the independency of the linear systems.
In our previous study, we developed a multi-GPU implementation of the complex moment based method for real symmetric dense problems using MAGMA and MPI. We extend the implementation for solving Hermitian and non-Hermitian problems.
Performance evaluations on HA-PACS, a GPU cluster which has nodes with four NVIDIA M2090s and two Sandy Bridge-EPs, will be shown.
Inge Gutheil (Forschungszentrum Jülich), Johannes Grotendorst (Forschungszentrum Jülich)
For new exascale computers the degree of parallelism will increase leading to architectures with more and more cores per node and multithreading and SIMD on each core. Due to the limited memory per node the pure MPI parallelizing strategy may be no longer suited for these new architectures.
For applications that already use a hybrid parallelization due to memory limits, a pure MPI implementation will waste several cores for the eigensolver unless a hybrid version can be used.
Newly developed libraries for dense linear algebra computation such as the ELPA library for the computation of a large part of the eigenspectrum of dense real symmetric and complex Hermitan matrices thus offer versions with hybrid MPI and OpenMP parallelization. On Intel architectures it has been shown that this hybrid parallelization can perform better than the pure MPI parallel version. On BlueGene/Q the hybrid version is still experimental, but it shows promising results although the pure MPI version using all cores still performs better.
In this talk we will present performance evaluation results of the two eigensolvers of the library ELPA on BlueGene/Q and compare it to the results on the Intel Nehalem cluster JUROPA.
Thomas Auckenthaler (TU München), Thomas Huckle (TU München), Roland Wittmann (TU München)
In this talk, we present a new stable algorithm for the parallel QR-decomposition of "tall and skinny" matrices. The algorithm has been developed for the dense symmetric eigensolver ELPA, whereat the QR-decomposition of tall and skinny matrices represents an important substep. Our new approach is based on the fast but unstable CholeskyQR algorithm. We show the stability of our new algorithm and provide promising results of our MPI-based implementation on different clusters.
Edoardo Di Napoli (Forschungszentrum Jülich), Mario Berljafa (University of Manchester)
Sequences of eigenvalue problems consistently appear in a large class
of applications based on the iterative solution of a non-linear
eigenvalue problem. A typical example is given by the chemistry and
materials science ab initio simulations relying on computational
methods developed within the framework of Density Functional Theory
(DFT). DFT provides the means to solve a high-dimensional quantum
mechanical problem by representing it as a non-linear generalized
eigenvalue problem which is solved self-consistently through a series
of successive outer-iteration cycles. As a consequence each
self-consistent simulation is made of several sequences of generalized
eigenproblems 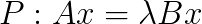 . Each sequence,
. Each sequence,  , groups together eigenproblems with increasing
outer-iteration index
, groups together eigenproblems with increasing
outer-iteration index  .
.
In more general terms a set of eigenvalue problems 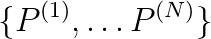 is said to be a “sequence” if the solution of the
is said to be a “sequence” if the solution of the
 -th eigenproblem determines, in an application-specific manner,
the initialization of the
-th eigenproblem determines, in an application-specific manner,
the initialization of the  -th eigenproblem. For instance at
the beginning of each DFT cycle an initial function
-th eigenproblem. For instance at
the beginning of each DFT cycle an initial function
 determines the initialization of the
determines the initialization of the
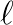 -th eigenproblem. A large fraction of
-th eigenproblem. A large fraction of 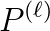 eigenpairs
are then use to compute a new
eigenpairs
are then use to compute a new  which, in
turn, leads to the initialization of a new eigenvalue problem
which, in
turn, leads to the initialization of a new eigenvalue problem
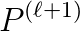 . In addition to be part of a sequence, successive
eigenproblems might possess a certain degree of correlation connecting
their respective eigenpairs. In DFT sequences, correlation becomes
manifest in the way eigenvectors of successive eigenproblems become
progressively more collinear to each other as the
. In addition to be part of a sequence, successive
eigenproblems might possess a certain degree of correlation connecting
their respective eigenpairs. In DFT sequences, correlation becomes
manifest in the way eigenvectors of successive eigenproblems become
progressively more collinear to each other as the 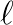 -index
increases.
-index
increases.
We developed a subspace iteration method (ChFSI) specifically tailored
for sequences of eigenproblems whose correlation appears in the form
of increasingly collinear eigenvectors. Our strategy is to take the maximal advantage possible from the
information that the solution of the 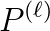 eigenproblem is
providing when solving for the successive
eigenproblem is
providing when solving for the successive 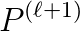 problem. As a
consequence the subspace iteration was augmented with a Chebyshev
polynomial filter whose degree gets dynamically optimized so as to
minimize the number of matrix-vector multiplications. The
effectiveness of the Chebyshev filter is substantially increased when
inputed the approximate eigenvectors
problem. As a
consequence the subspace iteration was augmented with a Chebyshev
polynomial filter whose degree gets dynamically optimized so as to
minimize the number of matrix-vector multiplications. The
effectiveness of the Chebyshev filter is substantially increased when
inputed the approximate eigenvectors 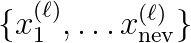 , as well as very reliable estimates, namely
, as well as very reliable estimates, namely
![[\lambda_1^{(\ell)},\ \lambda_{\rm nev}^{(\ell)}]](../img/eqn/5B5Clambda_15E7B285Cell297D2C5C205Clambda_7B5Crm20nev7D5E7B285Cell297D5D.png) , for the limits of
the eigenspectrum interval
, for the limits of
the eigenspectrum interval ![[a,\ b]](../img/eqn/5Ba2C5C20b5D.png) to be filtered in. In addition
the degree of the polynomial filter is adjusted so as to be minimal
with respect to the required tolerance for the eigenpairs
residual. This result is achieved by exploiting the dependence each
eigenpair residual have with respect to its convergence ratio as
determined by the rescaled Chebyshev polynomial and its
degree. The solver is complemented with an efficient mechanism which locks and
deflates the converged eigenpairs.
to be filtered in. In addition
the degree of the polynomial filter is adjusted so as to be minimal
with respect to the required tolerance for the eigenpairs
residual. This result is achieved by exploiting the dependence each
eigenpair residual have with respect to its convergence ratio as
determined by the rescaled Chebyshev polynomial and its
degree. The solver is complemented with an efficient mechanism which locks and
deflates the converged eigenpairs.
The resulting eigensolver was implemented in C language and parallelized for both shared and distributed architectures. Numerical tests show that, when the eigensolver is inputed approximate solutions instead of random vectors, it achieves up to a 5X speedup. Moreover ChFSI takes great advantage of computational resources by scaling over a large range of cores commensurate with the size of the eigenproblems. Specifically, by making better use of massively parallel architectures, the distributed memory version will allow DFT users to simulate physical systems quite larger than are currently accessible.
Andreas Stathopoulos (College of William and Mary), Lingfei Wu (College of William and Mary)
The Singular Value Decomposition (SVD) is a ubiquitous computational kernel in science and engineering. Many applications demand a few of the largest or smallest singular values of a large sparse matrix  and the associated left and right singular vectors. The computation of the smallest singular triplets in particular presents challenges both to the speed of convergence and the accuracy that iterative methods can accomplish. We focus mainly on this difficult problem.
and the associated left and right singular vectors. The computation of the smallest singular triplets in particular presents challenges both to the speed of convergence and the accuracy that iterative methods can accomplish. We focus mainly on this difficult problem.
While traditional solutions were based on symmetric eigenvalue methods, over the last two decades the bidiagonalization Lanczos method has gained a much wider acceptance. Although in its original form it suffered from orthogonality loss, large memory demands, and problems with extracting the singular vectors through classical Rayleigh Ritz, recent techniques for restarting, refined and harmonic projections, and blocking have significantly increased its robustness. Despite this remarkable progress, current Lanczos bidiagonalization methods are still in development. Existing MATLAB implementations serve mainly as a testbed for mathematical research, and are not close to a general, high performance code. More importantly, preconditioning techniques cannot be used directly.
The JDSVD is the only method currently that can exploit preconditioning directly for the SVD problem. It employs several of the above techniques for restarting and projection, but this also is available only as a MATLAB code. Moreover, it relies on the solution of the correction equation to achieve good convergence, but the system it solves is maximally indefinite and thus difficult to solve. On the other hand, if no inner iterations are performed and no preconditioning is used, the outer iteration of JDSVD is much slower than bidiagonalization Lanczos.
We argue that a well designed, state-of-the-art eigensolver such as PRIMME, can offer faster speed of convergence than both of the above methods, even without preconditioning, while also exploiting the highly optimized implementation to achieve superior performance on sequential and parallel architectures. To accomplish this, we have engineered a hybrid, two-stage algorithm that addresses performance and accuracy at two successive stages.
One of the stumbling blocks of bidiagonalization Lanczos and JDSVD methods have been the irregular convergence to the smallest singular values. The problem is accentuated with restarting since the relevant singular vector directions may be discarded and have to be built again. A careful combination of harmonic and refined projections alleviate this problem, but their implementation can be very expensive. In contrast, a symmetric eigenvalue solver applied to the normal equations converges monotonically toward the smallest eigenvalues. Moreover, efficient restarting schemes exist that can achieve near-optimal convergence. PRIMME provides such methods that equal the convergence of the unrestarted bidiagonalization Lanczos, for a fraction of memory and time. To extract the eigenpairs from the normal equations, however, a squared projection must be used which limits the maximum achievable accuracy for the smallest eigenpairs. The idea is that after most of the digits of accuracy have been obtained through a very fast method on the normal equations, we resolve the rest of the accuracy by switching to an interior eigenvalue problem on the augmented matrix using a highly tuned, Jacobi-Davidson method. The availability of excellent shifts for the correction equation acts as an iterative refinement with the additional benefit of subspace acceleration.
We present theoretical and experimental evidence for the merit of this approach, and emphasize that a highly optimized, preconditioned, parallel code for the SVD problem now exists.
Martin Köhler (Max Planck Institute for Dynamics of Complex Technical Systems), Peter Benner (Max Planck Institute for Dynamics of Complex Technical Systems), Jens Saak (Max Planck Institute for Dynamics of Complex Technical Systems)
The solutions of (generalized) Lyapunov equations play a key role in many applications in systems and control theory. Their robust numerical computation, when the full solution is sought, is considered solved since the seminal work of Bartels and Stewart. The algorithm consists mainly of two phases: a (quasi-)triangular reduction and a forward/backward substitution. A number of variants of what is now called the Bartels-Stewart algorithm have been proposed. Here, we focus on the second phase which consists mainly of BLAS level-2 directives and which is used in standard implementations, as e.g. the solver lyap in the MATLAB® Control Systems Toolbox (which is based upon the routine SG03AY from the systems and control library SLICOT). On modern computers, however, the formulation of BLAS level-3 type implementations is crucial to enable optimal usage of cache hierarchies and modern block scheduling methods, which are based on directed acyclic graphs describing the interdependence of single block computations.
Our contribution transforms the available level-2 variants for the solution of the (quasi-)triangular generalized Lyapunov equation to level-3 versions. Thus, by comparison on a standard multicore machine and selection of the most appropriate variant we can close the aforementioned gap in the implementations.
To this end, we analyze the implementation details of the current SLICOT version and identify the crucial operations which prevent a blocked implementation. We consider different algorithms to handle the arising generalized Sylvester equations and compare the flop counts and their performance on current computer architectures. Additionally, we focus on implementation details that avoid unnecessary computations and guarantee the symmetry of the solution of the Lyapunov equation. In a number of numerical experiments we point out which of the covered variants should replace the SLICOT implementation of the solver for (quasi-)triangular generalized Lyapunov equations with a comparable accuracy and much improved performance. Significant speed-ups over current standard solvers can be observed already for moderately sized Lyapunov equations.
Wilfried Gansterer (University of Vienna), Karl Prikopa (University of Vienna)
We present a novel truly distributed linear least squares solver PSDLS-IR for a rectangular matrix distributed row-wise. Upon termination, each node holds an approximation of the full solution vector. Since we are interested in a truly distributed algorithm, we do not employ a fusion centre or multi hop communication and limit the communication of each node to its immediate neighbourhood.
Mathematically, PSDLS-IR is based on the semi-normal equations (SNE). It is well known that SNE is in general not backward stable. In combination with iterative refinement the method can be stabilised. We consider mixed precision iterative refinement, which increases the performance of the algorithm because the computationally and communication intensive operations are reduced. This leads to a significant speed-up compared to existing truly distributed linear least squares solvers.
In PSDLS-IR, all communication between nodes takes place in the context of reduction operations. They can, for example, be performed using randomized gossip algorithms where each node only communicates with its immediate neighbourhood. Moreover, fault tolerant reduction algorithms become applicable. We focus on the push-sum algorithm and the fault tolerant push-flow algorithm. We analyse the communication cost of PSDLS-IR and compare it to existing distributed linear least squares solvers. Moreover, we summarize simulation experiments showing that our PSDLS-IR solver requires significantly fewer messages per node to reach a high accuracy solution than the existing methods.
Jonathan Hogg (Rutherford Appleton Laboratory), Evgueni Ovtchinnikov (Rutherford Appleton Laboratory), Jennifer Scott (Rutherford Appleton Laboratory)
The sparse LDL^T factorization of symmetric matrices is a key kernel in optimization methods. These methods often produce numerically challenging sparse indefinite matrices that require pivoting to obtain an accurate solution and estimate of the inertia.
We present a new GPU implementation of this kernel that includes full pivoting and performs all numerical operations on the GPU. This avoids the PCI-express bottleneck that has limited the effectiveness of such solvers in the past.
We also describe the use of some novel numerical techniques such as the use of a posteriori pivoting to minimize the overhead of pivot acceptance tests, and the use of a stable partial inverse of L to accelerate the solve phase.
Ioannis E. Venetis (University of Patras), Alexandros Kouris, Alexandros Sobczyk, Efstratios Gallopoulos (University of Patras), Ahmed Sameh (Purdue University)
Solving banded linear systems is an important computational kernel in many applications. Over the years, a variety of algorithms and modules in numerical libraries for this task have been proposed that are suitable for computer systems ranging from uniprocessors to multicores and high performance coprocessors. In this presentation we focus on tridiagonal systems as these are very common and are also encountered as kernels in several linear algebra computations. Interesting recent efforts focus on GPU implementations. Algorithms based on cyclic reduction, parallel cyclic reduction and recursive doubling and hybrids were studied in [4]; these depend on symmetric positive definiteness or diagonal dominance to proceed without breakdown.
For very large tridiagonal and narrow banded matrices, a well known approach for obtaining parallelism and high performance is to use partitioning. As shown recently by Chang et al., the Spike partitioning framework ([2, 3]) combined with a special pivoting algorithm for the resulting subsystems can lead to a scalable, highly performing tridiagonal solver [1].
In this presentation we revisit a Spike approach combined with Givens rotations to solve the subsystems, as first proposed in [3], present its CUDA implementation and evaluate its performance and stability.
[1] L.-W. Chang, J.A. Stratton, H.S. Kim, and W.-M.W. Hwu. A scalable, numerically stable, high-performance tridiagonal solver using GPUs. In Proc. Int'l. Conf. High Performance Computing, Networking Storage and Analysis, SC '12, pages 27:1-27:11, Los Alamitos, CA, USA, 2012. IEEE Computer Society Press. [2] E. Polizzi and A.H. Sameh. A parallel hybrid banded system solver: The SPIKE algorithm. Parallel Computing, 32(2):177-194, 2006. [3] A.H. Sameh and D.J. Kuck. On stable parallel linear system solvers. J. Assoc. Comput. Mach., 25(1):81-91, January 1978. [4] Y Zhang, Jonathan Cohen, and John D Owens. Fast tridiagonal solvers on the GPU. ACM Sigplan Notices, 45(5):127-136, 2010.
Bruno Carpentieri (University of Groningen), Jia Liao (University of Groningen), Masha Sosonkina (Old Dominion University ), Aldo Bonfiglioli (University of Basilicata)
The starting point for this project was the iterative solution of sparse and block structured linear systems that arise from the analysis of turbulent flows in computational fluid dynamics applications. In the last two years we have studied preconditioning techniques based on block multilevel incomplete LU factorization preconditioners for this problem class, and we have found them to be quite effective in reducing the number of GMRES iterations. These preconditioners exhibit better parallelism than standard ILU algorithms due to the recursive factorization and they may be noticeably more robust for comparable memory usage especially for solving large problems. Additionally, exploiting the available block structure in the matrix can maximize computational efficiency.
Sparse matrices arising from the solution of systems of partial differential equations often exhibit a perfect block structure, meaning that the nonzero blocks in the sparsity pattern are fully dense (and typically small), e.g., when several unknown quantities are associated with the same grid point. However, similar block orderings can be sometimes unravelled also on general unstructured matrices, by ordering consecutively rows and columns with a similar sparsity pattern, and treating some zero entries of the reordered matrix as nonzero elements, and the nonzero blocks as dense, with a little sacrifice of memory. The reordering results in linear systems with blocks of variable size in general.
Our recently developed parallel package pVBARMS (parallel variable block algebraic recursive multilevel solver) for distributed memory computers takes advantage of these frequently occurring structures in the design of the multilevel incomplete LU factorization preconditioner, and maximizes computational efficiency achieving increased throughput during the computation and improved reliability on realistic applications. The method detects automatically any existing block structure in the matrix without any user’s prior knowledge of the underlying problem, and exploits it to maximize computational efficiency.
We describe a novel parallel MPI-based implementation of pVBARMS for distributed memory computers based on the block Jacobi, the additive Schwarz and the Schur-complement methods. We address hybrid MPI and OpenMP implementations and gain further parallelism using Many-Integrated Codes (MIC) technology. Implementation details are always critical aspects to consider in the design of sparse matrix algorithms. Therefore, we revisit our original implementation of the partial (block) factorization step with a careful selection of the parameters, and we compare different algorithms for computing the block ordering based on either graph or matrix analysis.
Finally, we report on the numerical and parallel scalability of the pVBARMS package for solving turbulent Navier-Stokes equations on a suite of two- and three-dimensional test cases, among which the calculation of the flow past the DPW3-W1 wing configuration of the third AIAA Drag Prediction Workshop, which is the application that motivated this study. In our formulation the mean flow and turbulent transport equations are solved in coupled form using a Newton-Krylov algorithm. These analyses are carried with coarse- to medium-sized grids featuring up to 6.5 million nodes at Reynolds number equal to 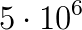 .
.
Ziad Sultan (University of Grenoble), Jean-Guillaume Dumas (University of Grenoble), Clément Pernet (University of Grenoble), Thierry Gautier (INRIA)
We propose efficient parallel algorithms and implementations of LU factorization over word size prime fields and target shared memory architectures. With respect to numerical linear algebra, we have identified three major differences, specific to exact linear algebra.
First, the arithmetic complexity could be dominated by modular reductions. Therefore, it is mandatory to delay as much as possible these reductions. Delaying the latter can be done by accumulating several multiplications before reducing while keeping the result exact. This induces splitting the matrices in blocks of large size to accumulate multiplication operations as much as possible, without overflow. Then one performs only one reduction operation for several of those accumulations. Simultaneously, to gain in parallelism, the splitting should mix fine-grain parallelizations of tiled iterative and recursive algorithms. A finer grain allows more flexibility in the scheduling when running numerous cores: different independent blocks can be treated at the same time. This trade-off also creates challenges on the efficiency of the underlying scheduler and on the minimization of distant memory accesses in order to reduce the dependency on the bus speed.
Second, in numerical linear algebra, the cost of arithmetic operations is more or less associative: with dimensions above a rather low threshold, sequential matrix multiplication of the BLAS reaches the peak efficiency of the processor. Hence the granularity has very little impact on the efficiency of a block algorithm run in sequential. Over a finite field numerical stability is not an issue, and asymptotically fast matrix multiplication algorithms, like Winograd's variant of Strassen's fast algorithm can be used on top of the BLAS. Their speed-up increases with matrix dimension. The cost of sequential matrix multiplication over finite field is therefore not associative: a larger granularity delivers better sequential efficiency. Thus, trade-offs are also to be made between size of blocks well suited to those fast variants or to load and communication balancing.
Third, many applications over finite fields require the rank profile of the matrix rather than the solution to a linear system. It is thus important to design parallel algorithms that preserve and compute this rank profile. This profile is a key invariant used in many applications using exact Gaussian elimination, such as Grobner basis computations and computational number theory. Now, in dense numerical linear algebra, pivoting is used to ensure good numerical stability and good data locality. In the context of exact linear algebra, only certain pivoting strategies will reveal the echelon form or, equivalently, the rank profile of the matrix. Moreover, the rank deficiency of some blocks also leads to unpredictable dimensions of the tiles or slabs as the rank profile is only discovered during the algorithm. Thus the computing load for each task is not known in advance (some panel blocks may have high rank deficiency), making the tasks very heterogeneous. The block splitting has then to be dynamically computed.
We thus propose and compare different parallelization strategies and block decomposition to tackle these issues: tile iterative with left-looking, right-looking and Crout variants with delayed modular reductions; slab and tile recursive variants; dynamic/static block cutting and adaptive coupling of the different variants. Experiments demonstrate that the tile recursive variant performs better and matches the performance of reference numerical software when no rank deficiency occur. Furthermore, even in the most heterogeneous case, namely when all pivot blocks are rank deficient, we show that it is possible to maintain a high efficiency.
Jiri Stary (Academy of Sciences of the Czech Republic), Radim Blaheta (Academy of Sciences of the Czech Republic), Ondrej Jakl (Technical University of Ostrava)
We deal with the solution of high resolution FEM systems arising from the analysis of the macroscale response of materials through investigation of processes in their microstructure. By other words, we test the smaller material samples with relatively complicated inner structure and try to determine effective (homogenized) material properties. In computational micromechanics, the testing of such samples means solution of boundary value problems on test domains involving the microstructure with loading provided by suitable boundary conditions.
We focus on X-ray CT image based micromechanics of geomaterials with the use of continuum mechanics and the finite element computation of the microscale strains and stresses. This means that basic information about the microstructure is provided by analysing (segmentation) of 3D images of real samples. This information should be completed by information on local material properties, i.e. material properties of the individual material constituents.
There is a strong need for high performance parallel computing at several stages of the computational micromechanics, namely at - analysis of CT scans, - high resolution finite element solution of boundary value problems, - solution of inverse problems for determination or calibration of local material properties.
In this contribution, we focus on the second point, i.e. solving the high resolution finite element systems with tens or hundreds degrees of freedom on available parallel computers at the Institute of Geonics and the IT4Innovations supercomputer centre in Ostrava. We describe efficiency of the in-house GEM solvers exploiting the Schwarz domain decomposition method with aggregation by performing computational experiments on the above parallel computers. The solution of these systems is also necessary for building efficient solution methods for inverse material identification problems.
Nam Zin Cho (KAIST), Han Jong Yoo (KAIST)
Nuclear reactor core analysis via neutron transport method in a three-dimensional whole-core domain is one of the challenges facing reactor physicists. Monte Carlo method is a stochastic method which is directly simulating particles with minimum assumptions. Method of characteristics (MOC) is a deterministic approach which is capable of analyzing heterogeneous geometry with energy groups. Both of these methods are computationally very expensive when applied directly to 3-D whole-core analysis. A typical nuclear reactor of current generation is radially very heterogeneous but is usually piecewise homogeneous in axial direction. As appropriate for this type of reactors, a 2D/1D fusion method was developed in the previous work for 3-D whole-core analysis, which employs two-dimensional method of characteristics in radial direction and one-dimensional SN-like method in axial direction. Both 2-D and 1-D problems are coupled by axial and radial leakage terms. With a small mesh size, however, these leakage terms may cause negative source term and ruin the convergence of the method. In this paper, a novel scheme of 3D/2D rotational plane slicing method is proposed for whole-core transport calculation. A 3-D problem is sliced along the characteristics line, forming multiple 2-D planes (characteristics planes). These 2-D planes usually consist of rectangular mesh cells in reactor core problems. Various 2-D SN solvers are available for these 2-D transport problems and the simplest diamond-difference (DD) scheme is chosen for this work. Parallel computing of this approach is efficient since each characteristic plane is independent from each other. The method is tested on several benchmark problems with encouraging results for accuracy and parallelization.
Remigijus Paulavičius (Vilnius University), Julius Žilinskas (Vilnius University)
The availability of computer power offers potential and challenges for solving difficult scientific optimization problems using global optimization algorithms. Many of these algorithms have large memory requirements and strong data dependency that degrade the program scalability and efficiency of parallel algorithms. Global optimization algorithms DIRECT (DIviding RECTangles) and DISIMPL (DIviding SIMPLices) are such kind of algorithms. This talk is concerned with a parallel implementation and the application of parallel algorithms to applied problems arising in civil engineering. Systems of linear equations often appear in computation of objective function and constraints of such problems. In our results we investigate the efficiency of parallel optimization algorithms for these problems.
Alvaro Frank (RWTH Aachen), Diego Fabregat-Traver (RWTH Aachen), Paolo Bientinesi (RWTH Aachen)
We present high-performance algorithms and implementations to
carry out Genome Wide Association Studies (GWAS) of omics data
on multi-threaded architectures.
GWAS study the relation between phenotype traits and genetic variations of
individuals, while the term omics typically implies large datasets
and large-scale analyses.
We consider a specific class of GWAS that rely on the
solution of billions of ordinary least squares (OLS) problems
 , where
, where
 determines the relation between a genetic marker
determines the relation between a genetic marker 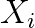 and a trait
and a trait 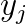 .
In GWAS, the above equation has to be solved for the cross product of
.
In GWAS, the above equation has to be solved for the cross product of  matrices
matrices  and
and 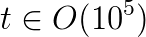 vectors
vectors  of size
of size 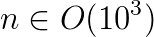 ,
resulting in the computation of the order of peta-floating point operations (petaflops)
over terabytes of data.
The proposed solvers deal with the high computational requirements of GWAS
efficiently, reducing considerably the required time to solution when
compared to existing solvers.
,
resulting in the computation of the order of peta-floating point operations (petaflops)
over terabytes of data.
The proposed solvers deal with the high computational requirements of GWAS
efficiently, reducing considerably the required time to solution when
compared to existing solvers.
Current solvers, based on either traditional libraries (e.g., LAPACK) or domain-specific ones (e.g., ProbABEL from the GenABEL suite), suffer from a number of limitations. The main one comes from the fact that these libraries solve individual OLS problems in isolation, which hinders their efficiency and scalability. Additionally, these solvers stream data from/to disk synchronously which, given the size of the involved datasets, adds a noticeable overhead. Our solvers overcome these shortcomings and are thus able to treat large problems in reduced time frames. First, we exploit application-specific knowledge, such as the correlation among problems and the properties of the matrices, to remove redundant computations and lower the computational cost of the entire analysis.
Then, we model and rearrange the required data transfers, and make use of out-of-core techniques so that input/output (I/O) is, when possible, completely overlapped with computation.
Finally, we merge the solution of multiple OLS problems to cast the bulk of the computation in terms of efficient BLAS-3 kernels, and combine the use of multi-threaded BLAS with OpenMP to attain scalability.
As the experiments show, our solvers attain a high efficiency (from 70% to 85% of the peak performance), and when executed on a 40-core machine, they attain a speedup of about 32x. Also, I/O overhead is successfully overlapped with computations. As a result, our routines outperform current state-of-the-art tools by a factor of 100.
Gemma Sanjuan Gomez (Autonomous University of Barcelona), Tomàs Margalef (Autonomous University of Barcelona), Ana Cortés (Autonomous University of Barcelona)
Forests fires are a significant problem especially in countries of the Mediterranean basin. To fight against these disasters, the accurate prediction of forest fire propagation is a crucial issue. Propagation models try to describe the future evolution of the forest fire given an initial scenario. However, the data describing the real fire scenario are usually subject to high levels of uncertainty. Moreover, there are input parameters that present spatial and temporal variation that make the prediction less accurate.
Wind speed and direction are parameters that affect forest fire propagation dramatically. So, an accurate estimation of such parameters is crucial to predict the fire propagation precisely. WindNinja is a wind field simulator that can easily be coupled to a forest fire propagation simulator such as FARSITE. However, wind field simulators present to main drawbacks when the map describing the terrain is large ( Km): On the one hand the execution time is prohibitive and, on the other hand, the amount of memory required to tackle such problem is usually not available in a single node. Both problems are related to the number of cells describing the terrain.
Km): On the one hand the execution time is prohibitive and, on the other hand, the amount of memory required to tackle such problem is usually not available in a single node. Both problems are related to the number of cells describing the terrain.
To evaluate the wind field WindNinja apply mass conservation equations on the terrain surface and the mesh describing the terrain grows with the map size. However, the matrix describing the physical equations is a sparse matrix that is represented using CSR representation method. WindNinja solves the system applying a conjugate gradient method with LU preconditioner that converges quite fast, but scale very badly since it cannot be parallelized. To overcome this problem and reduce execution time and memory requirements a Domain Decomposition method with non-overlapping, commonly called Schur method has been applied.
The Schur method is a graph partitioning mathematical method that can be used to to divide the mesh representing the terrain map. Partitioning the mesh implies a partitioning of the equation system. So, the matrix describing the system of equations is arranged in such a way that there are submatrices representing the local interactions within any mesh partition and another one describing the interactions in the borders of the partitions. In this way the systems to be solved are smaller and can be solved in parallel.
The Schur method has been implemented using the METIS library to partition the CSR matrix describing the whole system. This library includes load balancing facilities that automatically distribute the non-zero elements of the matrix among the different partitions. The resulting system is solved applying the PARDISO library. This library different solvers combining direct and iterative methods and it presents very good scalability on SMPs and clusters of SMPs. Taking advantatge of PARDISO features different solvers have been applied including direct methods and iterative methods such as conjugate gradient with and without preconditioner.
A significant point to be considered is that partitioning the mesh in more parts to exploit more parallelism implies an increase in the points in the borders and, therefore, the submatrix representing the interactions in the borders includes more terms and is larger. Larger matrices require more complexity and more number of iterations to converge. So, it is necessary to determine the optimal number of partition that exploits parallelism, but does not penalizes execution time due to the increase in the matrix representing the borders among the different partitions of the mesh. Therefore, a partitioning methodology has been developed to determine the best partitioning.
The results show that the application of the Schur method with the proposed partitioning reduces execution time significantly and offers a good scalability.
Wolfgang Bangerth (Texas A&M University)
Solving realistic, applied problems with the most modern numerical methods introduces many levels of complexity. In particular, one has to think about not just a single method, but a whole collection of algorithms: a single code may utilize fully adaptive, unstructured meshes; nonlinear, globalized solvers; algebraic multigrid and block preconditioners; and do all this on 1,000 processors or more with realistic material models.
Codes at this level of complexity can no longer be written from scratch. However, over the past decade, many high quality libraries have been developed that make writing advanced computational software simpler. In this talk, I will briefly introduce the deal. The finite element library (http://www.dealii.org) whose development I lead and show how it has enabled us to develop the ASPECT code (http://aspect.dealii.org) for simulation of convection in the earth mantle. I will discuss some of the results obtained with this code and comment on the lessons learned from developing this massively parallel code for the solution of a complex problem.